Question

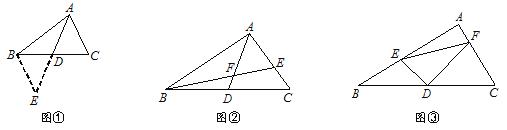
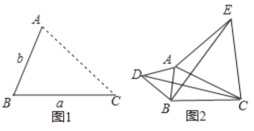
【题目】（1）发现：如图1，点A为线段BC外一动点，且BC=a，AB=b．当点A位于什么上时，线段AC的长取得最大值，且最大值为多少（用含a，b的式子表示）

（2）应用：点A为线段BC外一动点，且BC=4，AB=1，如图2所示，分别以AB，AC为边，作等边三角形ABD和等边三角形ACE，连接CD，BE．

①请找出图中与BE相等的线段，并说明理由；

②直接写出线段BE长的最大值．

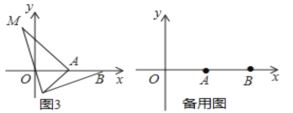
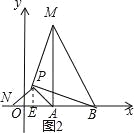
（3）拓展：如图3，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（6，0），点P为线段AB外一动点，且PA=2，PM=PB，∠BPM=90°，请直接写出线段AM长的最大值及此时点P的坐标．

Answer 1

【答案】（1）当点A位于CB的延长线上时，最大值为BC+AB=a+b，（2）①CD=BE，理由见解析；②最大值为BD+BC=AB+BC=5；（3）最大值为2+4，P（2﹣，）．

【解析】

（1）根据点A位于CB的延长线上时，线段AC的长取得最大值，即可得到结论；

（2）①根据等边三角形的性质得到AD=AB，AC=AE，∠BAD=∠CAE=60°，推出△CAD≌△EAB，根据全等三角形的性质得到CD=BE；②由于线段BE长的最大值=线段CD的最大值，根据（1）中的结论即可得到结果；

（3）连接BM，将△APM绕着点P顺时针旋转90°得到△PBN，连接AN，得到△APN是等腰直角三角形，根据全等三角形的性质得到PN=PA=2，BN=AM，根据当N在线段BA的延长线时，线段BN取得最大值，即可得到最大值为2+4；过P作PE⊥x轴于E，根据等腰直角三角形的性质，即可得到结论．

（1）∵点A为线段BC外一动点，且BC=a，AB=b，

∴当点A位于CB的延长线上时，线段AC的长取得最大值，且最大值为BC+AB=a+b，

（2）①CD=BE，

理由：∵△ABD与△ACE是等边三角形，

∴AD=AB，AC=AE，∠BAD=∠CAE=60°，

∴∠BAD+∠BAC=∠CAE+∠BAC，

即∠CAD=∠EAB，

在△CAD与△EAB中，

，

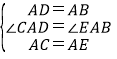∴△CAD≌△EAB，

∴CD=BE；

②∵线段BE长的最大值=线段CD的最大值，

由（1）知，当线段CD的长取得最大值时，点D在CB的延长线上，

∴最大值为BD+BC=AB+BC=5；

（3）∵将△APM绕着点P顺时针旋转90°得到△PBN，连接AN，

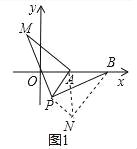
则△APN是等腰直角三角形，

∴PN=PA=2，BN=AM，

∵A的坐标为（2，0），点B的坐标为（6，0），

∴OA=2，OB=5，

∴AB=4，

∴线段AM长的最大值=线段BN长的最大值，

∴当N在线段BA的延长线时，线段BN取得最大值，

最大值=AB+AN，

∵AN=AP=2，

∴最大值为2+4；

如图2，过P作PE⊥x轴于E，

∵△APN是等腰直角三角形，

∴PE=AE=，

∴OE=BO﹣AB﹣AE=5﹣3﹣=2﹣，

∴P（2﹣，）．