题目内容
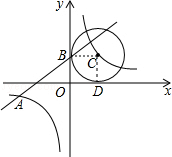
【题目】如图,已知一次函数y1=kx+b的图象与反比例函数y2= ![]() 的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=
的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2= ![]() 的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B 
(1)求m的值;
(2)求一次函数的表达式;
(3)根据图象,当y1<y2<0时,写出x的取值范围.
【答案】
(1)解:把点A(﹣4,m)的坐标代入y2= ![]() ,
,
则m= ![]() =﹣1,
=﹣1,
得m=﹣1;
(2)解:连接CB,CD,
∵⊙C与x轴,y轴相切于点D,B,
∴∠CBO=∠CDO=90°=∠BOD,BC=CD,
∴四边形BODC是正方形,
∴BO=OD=DC=CB,
∴设C(a,a)代入y2= ![]() 得:a2=4,
得:a2=4,
∵a>0,∴a=2,
∴C(2,2),B(0,2),
把A(﹣4,﹣1)和(0,2)的坐标代入y1=kx+b中,
得: ![]() ,
,
解得: ![]() ,
,
∴一次函数的表达式为:y1= ![]() x+2;
x+2;
(3)解:∵A(﹣4,﹣1),
∴当y1<y2<0时,x的取值范围是:x<﹣4.
【解析】(1)直接将A点代入反比例函数解析式求出答案;(2)直接利用切线的性质结合正方形的判定与性质得出C,B点坐标,进而利用待定系数法求出一次函数解析式;(3)利用A点坐标结合函数图象得出x的取值范围.

 阅读快车系列答案
阅读快车系列答案【题目】某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:
月产销量y(个) | … | 160 | 200 | 240 | 300 | … |
每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
(1)每月产销量y(个)与销售单价x(元)之间的函数关系式为; 从上表可知,每个玩具的固定成本Q(元)与月产销量y(个)之间满足反比例函数关系式,求出Q与y之间的关系式;
(2)若每个玩具的固定成本为30元,求它的销售单价是多少元?
(3)若该厂这种玩具的月产销量不超过400个,求此时销售单价最低为多少元?




