题目内容
【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为 . 
【答案】2 ![]() 或4﹣2
或4﹣2 ![]()
【解析】解:如图,当直线l在直线CE上方时,连接DE交直线l于M,
∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=BC,
∵AB=4,AD=BC=2,
∴AD=AE=EB=BC=2,
∴△ADE、△ECB是等腰直角三角形,
∴∠AED=∠BEC=45°,
∴∠DEC=90°,
∵l∥EC,
∴ED⊥l,
∴EM=2=AE,
∴点A、点M关于直线EF对称,
∵∠MDF=∠MFD=45°,
∴DM=MF=DE﹣EM=2 ![]() ﹣2,
﹣2,
∴DF= ![]() DM=4﹣2
DM=4﹣2 ![]() .
.
当直线l在直线EC下方时,
∵∠DEF1=∠BEF1=∠DF1E,
∴DF1=DE=2 ![]() ,
,
综上所述DF的长为2 ![]() 或4﹣2
或4﹣2 ![]() .
.
故答案为2 ![]() 或4﹣2
或4﹣2 ![]() .
.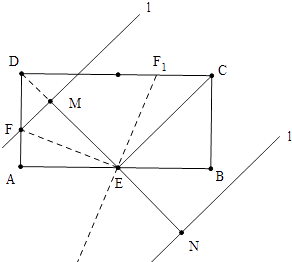
本题考查翻折变换、矩形的性质、等腰直角三角形的性质和判定,解题的关键是正确画出图形,注意有两种情形,属于中考常考题型.当直线l在直线CE上方时,连接DE交直线l于M,只要证明△DFM是等腰直角三角形即可利用DF= ![]() DM解决问题,当直线l在直线EC下方时,由∠DEF1=∠BEF1=∠DF1E,得到DF1=DE,由此即可解决问题.
DM解决问题,当直线l在直线EC下方时,由∠DEF1=∠BEF1=∠DF1E,得到DF1=DE,由此即可解决问题.

 阅读快车系列答案
阅读快车系列答案【题目】某校初三(1)班50名学生参加1分钟跳绳体育考试.1分钟跳绳次数与频数经统计后绘制出下面的频数分布表(60~70表示为大于等于60并且小于70)和扇形统计图.
等级 | 分数段 | 1分钟跳绳次数段 | 频数(人数) |
A | 120 | 254~300 | 0 |
110~120 | 224~254 | 3 | |
B | 100~110 | 194~224 | 9 |
90~100 | 164~194 | m | |
C | 80~90 | 148~164 | 12 |
70~80 | 132~148 | n | |
D | 60~70 | 116~132 | 2 |
0~60 | 0~116 | 0 |
(1)求m、n的值;
(2)求该班1分钟跳绳成绩在80分以上(含80分)的人数占全班人数的百分比;
(3)根据频数分布表估计该班学生1分钟跳绳的平均分大约是多少?并说明理由.