Question

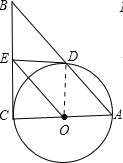
【题目】如图，已知正方形ABCD的边长为4，以点A为圆心，2为半径作圆，E是⊙A上的任意一点，将点E绕点D按逆时针方向转转90°得到点F，则线段AF的长的最小值____．

Answer 1

【答案】4.

【解析】

根据题意先证明△ADE≌△CDF，则CF=AE=1，根据三角形三边关系得：AF≤AC-CF，可知：当F在AC上时，AF最小，所以由勾股定理可得AC的长，可求得AF的最小值．

解：如图，连接FC，AC，AE．

∵ED⊥DF，
∴∠EDF=∠EDA+∠ADF=90°，
∵四边形ABCD是正方形，
∴AD=CD，∠ADC=90°，
∴∠ADF+∠CDF=90°，
∴∠EDA=∠CDF，
在△ADE和△CDF中，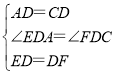

∴△ADE≌△CDF（SAS），
∴CF=AE=1，
∵正方形ABCD的边长为4，
∴AC=4，
∵AF≥AC-CF，
∴AF≥4-2
∴AF的最小值是4-2；
故答案为：4-2．