题目内容
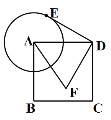
【题目】我们知道:有一内角为直角的三角形叫做直角三角形.类似地我们定义:有一内角为45°的三角形叫做半直角三角形.如图,在平面直角坐标系中,O为原点,A(4,0),B(-4,0),D是y轴上的一个动点,∠ADC=90°(A、D、C按顺时针方向排列), BC与经过A、B、D三点的⊙M交于点E,DE平分∠ADC,连结AE,BD.显然ΔDCE、ΔDEF、ΔDAE是半直角三角形.
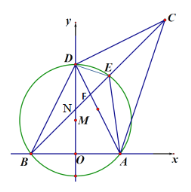
(1)求证:ΔABC是半直角三角形;
(2)求证:∠DEC=∠DEA;
(3)若点D的坐标为(0,8),求AE的长;
(4)BC交y轴于点N,问![]() 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
【答案】(1)见解析;(2)见解析;(3)![]() ;(4)
;(4)![]() 不变,为
不变,为 ![]() .
.
【解析】
(1)先求得∠ADE=45°,由同弧所对的圆周角可知:∠ABE=∠ADE=45°,根据定义得:△ABC是半直角三角形;
(2)根据垂直平分线的性质得:AD=BD,由等角对等边得:∠DAB=∠DBA,由D、B、A、E四点共圆,
则∠DBA+∠DEA=180°,可得结论;
(3)设⊙M的半径为r,根据勾股定理列方程为:(8-r)2+42=r2,可得⊙M的半径为5,由同弧所对的圆心角和圆周角的关系可得∠EMA=2∠ABE=90°,根据勾股定理可得结论;
(4)过点C作CH⊥DO于H,过点C作CQ⊥BA于Q,通过证明Rt△HDC≌Rt△ADO,推出HC=OD,DH=OA,推出CQ= BQ,得出∠CBQ=45°,推出△HCN为等腰直角三角形即可.
解:(1)∵∠ADC=90°,DE平分∠ADC,
∴∠ABE=∠ADE=45
∴ΔABC是半直角三角形
(2))∵OM⊥AB,OA=OB,
∴AD=BD,
∴∠DAB=∠DBA,
∵∠DEB=∠DAB,
∴∠DBA=∠DEB,
∵D、B、A、E四点共圆,
∴∠DBA+∠DEA=180°,
∵∠DEB+∠DEC=180°,
∴∠DEA=∠DEC;
(3))①如图,连接AM,ME,设⊙M的半径为r,
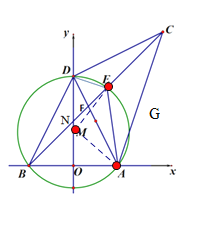
∵点D的坐标为(0,8)∴OM=8-r
由![]() 得
得![]() 解得r=5 ∴⊙M 的半径为5
解得r=5 ∴⊙M 的半径为5
∵∠ABE=45°
∴∠EMA=2∠ABE=90°,
∴EA2=MA2+ME2=52+52=50
∴![]()
(4)![]() 不变,为
不变,为 ![]()
过点C作CH⊥DO于H,过点C作CQ⊥BA于Q,
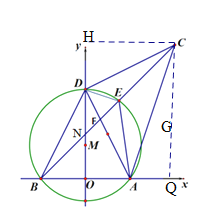
∵∠CDH+∠ODA=90°,∠CDH+∠CDH=90°,
∴∠ODA=∠CDA,
在△HDC和△ADO中,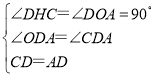
∴Rt△HDC≌Rt△ADO(AAS),
∴HC=OD,DH=OA,
又∵BO=AO,
∴HO=DH+DO=OB+CH,
而
∴CQ=OB+OQ=BQ,
∴∠CBQ=45°,
又∵CH∥BA,
∴∠HCN=45°,
∴△HCN为等腰直角三角形,
∴![]()
∴![]() =
=![]()

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案