题目内容
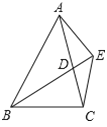
【题目】如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②AC=2CD;③AD=AE=EC;④∠BCE+∠BCD=180°.其中正确的是
A. ①②③ B. ①②④ C. ①③④ D. ②③④
【答案】C
【解析】已知BD为△ABC的角平分线,根据角平分线的定义可得∠ABD=∠CBD,在△ABD和△EBC中,BD=BC,∠ABD=∠CBD,BE=BA,由SAS可判定△ABD≌△EBC,即可得①正确;根据已知条件,无法证明AC=2CD,②错误; 已知BD为△ABC的角平分线,BD=BC,BE=BA,可得∠BCD=∠BDC=∠BAE=∠BEA, 再由∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠BCD=∠BEA,可得∠DCE=∠DAE,所以AE=EC;再由△ABD≌△EBC,可得AD=EC,所以AD=AE=EC,即③正确;由△ABD≌△EBC,可得∠BCE=∠BDA,所以∠BCE+∠BCD=∠BDA+∠BDC=180°,④正确.故选C.

练习册系列答案
相关题目