题目内容
【题目】如下图：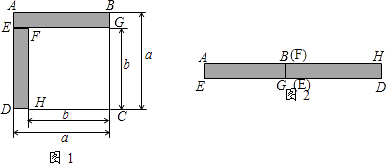 
（1）如图1，已知正方形ABCD的边长为a，正方形FGCH的边长为b，长方形ABGE和EFHD为阴影部分，则阴影部分的面积是（写成平方差的形式）
（2）将图1中的长方形ABGE和EFHD剪下来，拼成图2所示的长方形，则长方形AHDE的面积是（写成多项式相乘的形式）
（3）比较图1与图2的阴影部分的面积，可得乘法公式 ．
（4）利用所得公式计算：2（1+ 
）（1+ 
）（1+ 
）（1+ 
）+ 
．
【答案】
（1）a2﹣b2
（2）（a+b）（a﹣b）
（3）（a+b）（a﹣b）=a2﹣b2
（4）解：原式=4（1﹣ 
）（1+ ）（1+ 
）（1+ 
）（1+ 
）+ 
=4（1﹣ ）（1+ ）（1+ ）（1+ ）+
=4（1﹣ ）（1+ ）（1+ ）+
=4（1﹣ ）（1+ ）+
=4（1﹣ 
）+
=4﹣ +
=4．
【解析】解：（1）根据题意得：阴影部分面积为a2﹣b2；（2）根据题意得：阴影部分面积为（a+b）（a﹣b）；（3）可得（a+b）（a﹣b）=a2﹣b2； 所以答案是：（1）a2﹣b2；（2）（a+b）（a﹣b）；（3）（a+b）（a﹣b）=a2﹣b2
练习册系列答案
相关题目
