Question

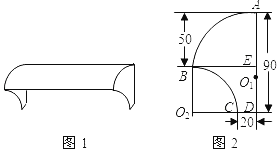
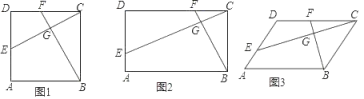
【题目】（1）如图1，正方形ABCD中，E、F分别是AD、DC边上的点，CE与BF交于点G，BF⊥CE，求证：BF＝CE；

（2）如图2，矩形ABCD中，AB＝2AD，E、F分别是AD、DC边上的点，CE与BF交于点G，∠A+∠BGE＝180°，求证：CE＝2BF；

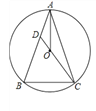
（3）如图3，若（2）中的四边形ABCD是平行四边形，且∠A＜90°，则CE＝2BF是否仍然成立？若成立，请证明；若不成立，请说明理由．

Answer 1

【答案】（1）见解析；（2）见解析；（3）成立，证明见解析.

【解析】

（1）只要证明△CDE≌△BCF，即可解决问题；

（2）先根据∠CFG+∠DCE＝90°，∠CED+∠DCE＝90°，判断出∠CFB＝∠DEC，进而得出△CDE∽△BCF，即可得出结论；

（3）先判断出∠BFC＝∠BCG，进而得出△BCG∽△BFC，即，再判断出△CFG∽△CED，得出，即可得出结论；

（1）如图1中，

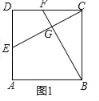
∵四边形ABCD是正方形，

∴CD＝BC，∠D＝∠BCF＝90°，

∵BF⊥CE，

∴∠BGC＝90°，

∴∠CBF+∠BCG＝90°，∠BCG+∠DCE＝90°，

∴∠DCE＝∠CBF，

∴△CDE≌△BCF，

∴BF＝CE

（2）如图2中，

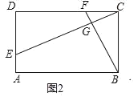
∵四边形ABCD是矩形，

∴CD＝AB，BC＝AD，∠A＝∠D＝∠BCD＝90°，

∵AB＝2AD，

∴CD＝2BC，

∵∠A+∠BGE＝180°，

∴∠CGF＝∠BGE＝90°＝∠D，

∴∠CFG+∠DCE＝90°，

∵∠CED+∠DCE＝90°，

∴∠CFB＝∠DEC，

∵∠D＝∠BCF，

∴△CDE∽△BCF，

∴＝2，

∴CE＝2BF；

（3）如图3中，

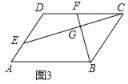
∵四边形ABCD是平行四边形，

∴∠A＝∠BCD，CD＝AB，BC＝AD，

∵AB＝2AD，

∴CD＝2BC，

∵∠A+∠BGE＝180°，∠BGE+∠BGC＝180°，

∴∠BGC＝∠A＝∠BCD，

∵∠BGC＝∠BFC+∠FCG，∠BCD＝∠BCG+∠FCG，

∴∠BFC＝∠BCG，

∵∠CBF＝∠FBC，

∴△BCG∽△BFC，

∴，

∵∠A+∠D＝180°，∠A+∠CGF＝180°，

∴∠D＝∠CGF，

∵∠FCG＝∠ECD，

∴△CFG∽△CED，

∴，

∴，

∴，

∵CD＝2BC，

∴CE＝2BF.