Question

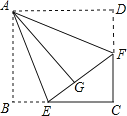
【题目】如图，正方形纸片ABCD的边长为3，点E、F分别在边BC、CD上，将AB、AD分别沿AE、AF折叠，点B、D恰好都落在点G处，已知BE=1，求EF的长.

Answer 1

【答案】

【解析】分析：由正方形纸片ABCD的边长为3，可得∠C=90°，BC=CD=3，由根据折叠的性质得：EG=BE=1，GF=DF，然后设DF=x，在Rt△EFC中，由勾股定理EF2=EC2+FC2，即可得方程，解方程即可求得答案．

详解∵正方形纸片ABCD的边长为3，∴∠C=90°，BC=CD=3.

根据折叠的性质得：EG=BE=1，GF=DF.

设DF=x，则EF=EG＋GF=1＋x，FC=DC－DF=3－x，EC=BC－BE=3－1=2.

在Rt△EFC中，EF2=EC2＋FC2，即（x＋1）2=22＋（3－x）2，

解得：.

∴DF= ，EF=1＋