题目内容
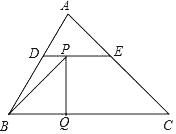
【题目】如图,在△ABC中,∠ABC=60°,∠C=45°,点D,E分别为边AB,AC上的点,且DE∥BC,BD=DE=2,CE=![]() ,BC=
,BC=![]() .动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ⊥BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )
.动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ⊥BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )
A. 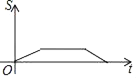 B.
B. 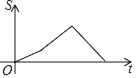
C. 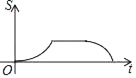 D.
D. 
【答案】D
【解析】
当P点在BD上运动时,BD=t,由∠ABC=60°得△BPQ的底BQ=t·cos60°=![]() ,
,
高PQ= t·sin60°=![]() ,故面积为S=
,故面积为S=![]() =
=![]() ,故为二次函数,当P点在BE上运动时,高PQ=
,故为二次函数,当P点在BE上运动时,高PQ=![]() 不变,底BQ为BD ·cos60°+DP=1+(t-2)=t-1,故面积S=
不变,底BQ为BD ·cos60°+DP=1+(t-2)=t-1,故面积S=![]() =
=![]() ,为一次函数,由此即可选出.
,为一次函数,由此即可选出.
当P点在BD上运动时,BD=t,
∵∠ABC=60°
∴BQ=t·cos60°=![]() ,
,
PQ= t·sin60°=![]() ,
,
∴为S=![]() =
=![]() ,为二次函数,
,为二次函数,
当P点在BE上运动时,高PQ=![]() 不变,
不变,
BQ=BD ·cos60°+DP=1+(t-2)=t-1,
∴S=![]() =
=![]() ,
,
为一次函数,由此即可选出.
故选D.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案【题目】为了传承中华优秀传统文化,某校组织八年级学生参加了“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,绘制如下不完整的条形统计图.
汉字听写大赛成绩分数段统计表
分数段 | 频数 |
| 2 |
| 6 |
| 9 |
| 18 |
| 15 |
汉字听写大赛成绩分数段条形统计图

(1)补全条形统计图.
(2)这次抽取的学生成绩的中位数在________的分数段中;这次抽取的学生成绩在![]() 的分数段的人数占抽取人数的百分比是_______.
的分数段的人数占抽取人数的百分比是_______.
(3)若该校八年级一共有学生350名,成绩在90分以上(含90分)为“优”,则八年级参加这次比赛的学生中成绩“优”等的约有多少人?