Question

【题目】根据卫生防疫部门要求，游泳池必须定期换水，清洗．某游泳池周五早上8：00打开排水孔开始排水，排水孔的排水速度保持不变，期间因清洗游泳池需要暂停排水，游泳池的水在11：30全部排完．游泳池内的水量Q（m2）和开始排水后的时间t（h）之间的函数图象如图所示，根据图象解答下列问题：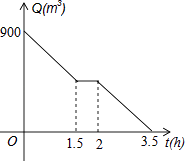

（1）暂停排水需要多少时间？排水孔排水速度是多少？
（2）当2≤t≤3.5时，求Q关于t的函数表达式．

Answer 1

【答案】
（1）解：暂停排水需要的时间为：2﹣1.5=0.5（小时）．

∵排水数据为：3.5﹣0.5=3（小时），一共排水900m3，

∴排水孔排水速度是：900÷3=300m3/h；

（2）解：当2≤t≤3.5时，设Q关于t的函数表达式为Q=kt+b，易知图象过点（3.5，0）．

∵t=1.5时，排水300×1.5=450，此时Q=900﹣450=450，

∴（2，450）在直线Q=kt+b上；

把（2，450），（3.5，0）代入Q=kt+b，

得 ，解得 ，

∴Q关于t的函数表达式为Q=﹣300t+1050．

【解析】本题考查了一次函数的应用，主要考查学生能否把实际问题转化成数学问题，题目比较典型，是一道比较好的题目．（1）暂停排水时，游泳池内的水量Q保持不变，图象为平行于横轴的一条线段，由此得出暂停排水需要的时间；由图象可知，该游泳池3个小时排水900（m3），根据速度公式求出排水速度即可；（2）当2≤t≤3.5时，设Q关于t的函数表达式为Q=kt+b，易知图象过点（3.5，0），再求出（2，450）在直线y=kt+b上，然后利用待定系数法求出表达式即可．