题目内容
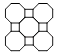
【题目】如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S1和S2，比较S1与S2的大小（ ）
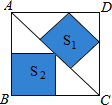
A. S1＞S2 B. S1=S2 C. S1＜S2 D. 不能确定
【答案】C
【解析】试题解析：如图，
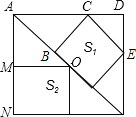
设正方形S1的边长为x，
∵△ANH和△HDG都为等腰直角三角形，
∴AN=NH，DH=DG，∠ANH=∠D=90°，
∴sin∠CAB=sin45°=
，即AH=
NH，同理可得：NH=HG=GD，
∴AH=NH=2HD，又AD=AH+HD=6，
∴HD=
=2，
∴HG2=22+22，即HG=2；
∴S1的面积为HG2=8；
∵∠MAO=∠MOA=45°，
∴AM=MO，
∵MO=MN，
∴AM=MB，
∴M为AB的中点，
∴S2的边长为3，
∴S2的面积为3×3=9，
∴S1＜S2．
故选C．
练习册系列答案
一线名师提优试卷系列答案
相关题目
【题目】某学习小组的同学做摸球实验时，在一个暗箱里放了多个只有颜色不同的小球，将小球搅匀后任意摸出一个，记下颜色并放回暗箱，再次将球搅匀后任意摸出一个，不断重复．下表是实验过程中记录的数据：
摸球的次数m | 300 | 400 | 500 | 800 | 1000 |
摸到白球的次数n | 186 | 242 | 296 | 483 | 599 |
摸到白球的频率 | 0.620 | 0.605 | 0.592 | 0.604 | 0.599 |
请估计从暗箱中任意摸出一个球是白球的概率是 ．
