题目内容
【题目】如图,在△ABC中,∠ACB=90°,点D是AB的中点,过点D作DE⊥AC于点E, 延长DE到点F,使得EF=DE,连接AF,CF.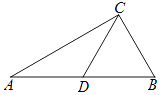
(1)根据题意,补全图形;
(2)求证:四边形ADCF是菱形;
(3)若AB=8,∠BAC=30°,求菱形ADCF的面积.
【答案】
(1)解:如图所示.

(2)证明:∵DE⊥AC,
∴∠AED=∠ACB=90°,
∴DE∥BC,
∵AD=DB,
∴AE=EC,∵ED=EF,
∴四边形ADCF是平行四边形,
∵AC⊥DF,
∴四边形ADCF是菱形.
(3)解:在Rt△ACB中,∵AB=8,∠BAC=30°,
∴BC= ![]() AB=4,AC=
AB=4,AC= ![]() BC=4
BC=4 ![]() ,
,
∵AE=EC,AD=DB,
∴DE= ![]() BC=2,
BC=2,
∴DF=2DE=4,
∴S菱形ADCF= ![]() ACDF=
ACDF= ![]() ×4
×4 ![]() ×4=8
×4=8 ![]() .
.
【解析】(1)根据题意画出图形即可;(2)首先证明AE=CE,DE=EF,推出四边形ADCF是平行四边形,再根据AC⊥DF,推出四边形ADCF是菱形;(3)求出菱形的对角线的长即可解决问题.
【考点精析】解答此题的关键在于理解直角三角形斜边上的中线的相关知识,掌握直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目