题目内容
【题目】如图，已知
，
，
，记
，则
________.
【答案】
【解析】
连接AC，设∠EAF＝x°，∠ECF＝y°，∠EAB＝4x°，∠ECD＝4y°，根据平行线性质得出∠BAC＋∠ACD＝180°，求出∠CAE＋∠ACE＝180°（4x°＋4y°），求出∠AEC＝4（x°＋y°），∠AFC═3（x°＋y°），即可得出答案．
证明：连接AC，
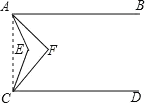
设∠EAF＝x°，∠ECF＝y°，∠EAB＝4x°，∠ECD＝4y°，
∵AB∥CD，
∴∠BAC＋∠ACD＝180°，
∴∠CAE＋4x°＋∠ACE＋4y°＝180°，
∴∠CAE＋∠ACE＝180°（4x°＋4y°），∠FAC＋∠FCA＝180°（3x°＋3y°）
∴∠AEC＝180°（∠CAE＋∠ACE）
＝180°[180°（4x°＋4y°）]
＝4x°＋4y°
＝4（x°＋y°），
∠AFC＝180°（∠FAC＋∠FCA）
＝180°[180°（3x°＋3y°）]
＝3x°＋3y°
＝3（x°＋y°），
∴∠AFC＝∠AEC．
即
.
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
