��Ŀ����
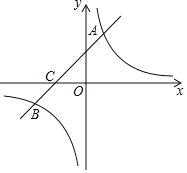
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=a��x��2��2��4��y�ύ�ڵ�A������ΪB����A������Ϊ��0����2������C���������ϣ������A��B�غϣ�������C��y��Ĵ��߽��������ڵ�D������AC��AD��CD�����C�ĺ�����Ϊm��
��1������������������Ӧ�ĺ�������ʽ��
��2���ú�m�Ĵ���ʽ��ʾ�߶�CD�ij���
��3����E�������߶Գ�����һ�㣬�ҵ�E��������ȵ�C��������С1������BD��DE������ACD�����ΪS1����BDE�����ΪS2����S1S2��0����S2=![]() S1ʱm��ֵ��
S1ʱm��ֵ��
��4����������y=a��x��2��2��4��x=2ƽ�ƣ��õ�������y=a��x��2��2+k������C��y��ƽ������������y=a��x��2��2+k���ڵ�F����CD��y�ύ�ڵ�G����CD=6��ֱ��д��ʹAC=FG�ĵ�F�����꣮
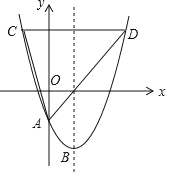
���𰸡���1��y=![]() x2��2x��2����2����m��2����m��0ʱ��CD=4��2m����m��2ʱ��CD=2m��4����3��m=2��
x2��2x��2����2����m��2����m��0ʱ��CD=4��2m����m��2ʱ��CD=2m��4����3��m=2��![]() ��m=
��m=![]() ����4����F����������1����2����1��3����5����2����5��3��
����4����F����������1����2����1��3����5����2����5��3��
�������������������1����A��0��-2����������������a=![]() ���ɣ�
���ɣ�
��2�������ߵĶԳ���Ϊֱ��x=2���ҵ�C�ĺ�����Ϊm���ó���m<2����m��0ʱ��CD=4-2m����m>2ʱ��CD=2m-4��
��3�����BE=![]() m2-2m+1��BE=-
m2-2m+1��BE=-![]() m2+2m-1���������������ϵ�ó����̣��ⷽ�̼��ɣ�
m2+2m-1���������������ϵ�ó����̣��ⷽ�̼��ɣ�
��4��������ó����ı���AGCF�Ǿ��Σ������C�����꣬��������ۣ����ݵ�������ϵ���ɵó��𰸣�
�����������1����������y=a��x��2��2��4��y�ύ�ڵ�A��0����2����
����2=4a��4��
��ã�a=![]() ��
��
����������������Ӧ�ĺ�������ʽΪy=![]() ��x��2��2��4��
��x��2��2��4��
��y=![]() x2��2x��2��
x2��2x��2��
��2����������y=![]() ��x��2��2��4�ĶԳ���Ϊֱ��x=2���ҵ�C�ĺ�����Ϊm��
��x��2��2��4�ĶԳ���Ϊֱ��x=2���ҵ�C�ĺ�����Ϊm��
�൱m��2����m��0ʱ��CD=4��2m��
��m��2ʱ��CD=2m��4��
��3����B��2����4����E��2�� ![]() m2��2m��3����
m2��2m��3����
��BE=![]() m2��2m+1��BE=��
m2��2m+1��BE=��![]() m2+2m��1��
m2+2m��1��
��S1=![]() CD��
CD��![]() m2��2m����S1=
m2��2m����S1=![]() CD����
CD����![]()
![]() CD��
CD��![]() m2��2m+1����S2=
m2��2m+1����S2=![]() CD����
CD����![]() m2+2m��1����
m2+2m��1����
��S2=![]() S1��
S1��
��4��![]() m2��2m��=3��
m2��2m��=3��![]() m2��2m+1������4��
m2��2m+1������4��![]() m2��2m��=��3��
m2��2m��=��3��![]() m2��2m+1����
m2��2m+1����
��ã�m=2��![]() ��=
��=![]() ��
��
��4����AC=FG������AF�����ı���AGCF�Ǿ��Σ�
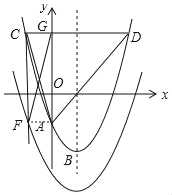
��CD=6�������ߵĶԳ���Ϊx=2��
���C�ĺ�����Ϊ��1��5��
�ٵ���C�ĺ�����Ϊ��1ʱ����C��������=![]() ������1��2��2������1����2=
������1��2��2������1����2=![]() ��
��
������������ƽ��ʱ����ͼ��ʾ��
�ߵ�A������Ϊ��0����2����
���F����������1����2����
������������ƽ��ʱ��ͬ���ó���F������Ϊ����1��3����
�ڵ���C�ĺ�����Ϊ5ʱ����C��������Ϊ![]() ��
��
������������ƽ��ʱ��ͬ���ĵ�F������Ϊ��5����2����
������������ƽ��ʱ��ͬ���ó���F������Ϊ��5��3����
������������F����������1����2����1��3����5����2����5��3����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�