题目内容
【题目】已知如图1，在以O为原点的平面直角坐标系中，抛物线y= 
x2+bx+c与x轴交于A、B两点，与y轴交于点C（0，﹣1），连接AC，AO=2CO，直线l过点G（0，t）且平行于x轴，t＜﹣1，
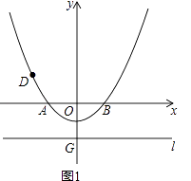
（1）求抛物线对应的二次函数的解析式；
（2）若D为抛物线y= x2+bx+c上一动点，是否存在直线l使得点D到直线l的距离与OD的长恒相等？若存在，求出此时t的值；
（3）如图2，若E、F为上述抛物线上的两个动点，且EF=8，线段EF的中点为M，求点M纵坐标的最小值．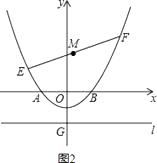
【答案】
（1）
解：∵c（0，﹣1），
∴y= 
x2+bx﹣1，
又∵AO=2OC，
∴点A坐标为（﹣2，0），
代入得：1﹣2b﹣1=0，
解得：b=0，
∴解析式为：y= x2﹣1
（2）
解：假设存在直线l使得点D到直线l的距离与OD的长恒相等，
设D（a， a2﹣1），
则OD= 
= 
= a2+1，
点D到直线l的距离： a2﹣1+|t|，
∴ a2﹣1+|t|= a2+1，
解得：|t|=2，
∵t＜﹣1，
∴t=﹣2，
故当t=﹣2时，直线l使得点D到直线l的距离与OD的长恒相等
（3）
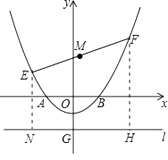
解：作EN⊥直线l于点N，FH⊥直线l于点H，
设E（x1，y1），F（x2，y2），
则EN=y1+2，FH=y2+2，
∵M为EF中点，
∴M纵坐标为： 
= 
= 
﹣2，
由（2）得：EN=OE，FH=OF，
∴ = ﹣2= 
﹣2，
要使M纵坐标最小，即 ﹣2最小，
当EF过点O时，OE+OF最小，最小值为8，
∴M纵坐标最小值为 ﹣2= 
﹣2=2．
【解析】（1）根据点C坐标，可得c=﹣1，然后根据AO=2CO，可得出点A坐标，将点A坐标代入求出b值，即可得出函数解析式；（2）假设存在直线l使得点D到直线l的距离与OD的长恒相等，设出点D坐标，分别求出OD和点D到直线l的距离，然后列出等式求出t的值；（3）作EN⊥直线l于点G，FH⊥直线l于点H，设出点E、F坐标，表示出点M的纵坐标，根据（2）中得出的结果，代入结果求出M纵坐标的最小值．
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点，以及对二次函数的性质的理解，了解增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
