题目内容
【题目】如图,在菱形ABCD中,∠B=60°,对角线AC平分角∠BAD,点P是△ABC内一点,连接PA、PB、PC,若PA=6,PB=8,PC=10,则菱形ABCD的面积等于_____.

【答案】50![]() +72
+72
【解析】
将线段AP绕点A顺时针旋转60°得到线段AM,连接PM,想办法证明∠APH=30°,利用勾股定理求出AB的平方即可解决问题.
将线段AP绕点A顺时针旋转60°得到线段AM,连接PM,作AH⊥BP于H.
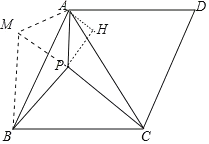
∵四边形ABCD是菱形,
∴AB=BC,
∵∠ABC=60°,
∴△ABC是等边三角形,
∵AM=AP,∠MAP=60°,
∴△AMP是等边三角形,
∵∠MAP=∠BAC,
∴∠MAB=∠PAC,
∴△MAB≌△PAC,
∴BM=PC=10,
∵PM2+PB2=100,BM2=100,
∴PM2+PB2=BM2,
∴∠MPB=90°,
∵∠APM=60°,
∴∠APB=150°,∠APH=30°,
∴AH=![]() PA=3,PH=
PA=3,PH=![]() ,BH=8+
,BH=8+![]() ,
,
∴AB2=AH2+BH2=100+48![]() ,
,
∴菱形ABCD的面积=2△ABC的面积=2×![]() ×AB2=50
×AB2=50![]() +72,
+72,
故答案为:50![]() +72.
+72.

练习册系列答案
相关题目