题目内容
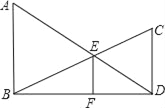
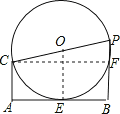
【题目】如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为 .

【答案】![]() .
.
【解析】
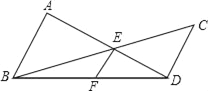
试题分析:首先判断当AB与⊙O相切时,PB的值最大,设AB与⊙O相切于E,连接OE,则OE⊥AB,过点C作CF⊥PB于F,由CA⊥AB,DB⊥AB,得到AC∥OE∥PB,四边形ABPC是矩形,证得CF=AB=6,在直角三角形PCF中,由勾股定理列方程求解.
试题解析:当AB与⊙O相切时,PB的值最大,
如图,设AB与⊙O相切于E,连接OE,则OE⊥AB,
过点C作CF⊥PB于F,
∵CA⊥AB,DB⊥AB,
∴AC∥OE∥PB,
四边形ABPC是矩形,
∴CF=AB=6,
∵CO=OP,
∴AE=BE,
设PB=x,则PC=2OE=2+x,PF=x-2,
∴(x+2)2=(x-2)2+62,
解得;x=![]() ,
,
∴BP最大值为:![]() .
.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目