题目内容
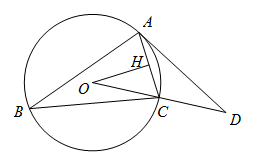
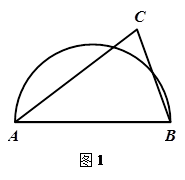
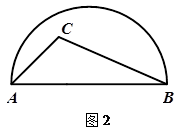
已知:如图,△ABC内接于⊙O,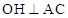 于H,
于H, ,过A点的直线与OC的延长线交于点D,
,过A点的直线与OC的延长线交于点D,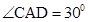 ,
,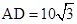 .
.
(1)求证:AD是⊙O的切线;
(2)若E为⊙O上一动点,连接AE交直线OD于点P,问:是否存在点P,使得PA+PH的值最小,若存在求PA+PH的最小值,若不存在,说明理由.
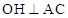 于H,
于H, ,过A点的直线与OC的延长线交于点D,
,过A点的直线与OC的延长线交于点D,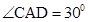 ,
,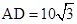 .
.(1)求证:AD是⊙O的切线;
(2)若E为⊙O上一动点,连接AE交直线OD于点P,问:是否存在点P,使得PA+PH的值最小,若存在求PA+PH的最小值,若不存在,说明理由.

(1)证明见解析;(2)存在, .
.
 .
.试题分析:(1)连接AO,求证
 即可.
即可.(2)求出OH的长,作A关于OD的对称点F,连接FH交OD于点P,根据对称性及两点之间线段最短可知此点P使PA+PH的值最小.
(1)如图,连接AO.
∵
 ,∴
,∴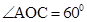 .
.∵AO=CO,∴
 .∴
.∴ .
.∴AD是⊙O的切线 .

(2)存在.
∵
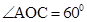 ,OA=OC,∴
,OA=OC,∴ AOC为等边三角形.
AOC为等边三角形.在Rt
 AOD中,∵
AOD中,∵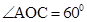 ,
,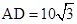 ,∴
,∴ .
.∵
 ,∴
,∴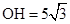 .
.如图,作A关于OD的对称点F,连接FH交OD于点P,根据对称性及两点之间线段最短可知此点P使PA+PH的值最小.
∴
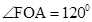 .∴
.∴ .
.∵
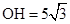 ,OF=10,∴
,OF=10,∴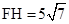 ,即PA+PH的最小值为
,即PA+PH的最小值为 .
.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
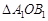 .
.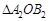 ,并判断
,并判断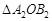 在位置上有何关系?若成中心对称,请直接写出对称中心坐标;如成轴对称,请直接写出对称轴的函数关系式.
在位置上有何关系?若成中心对称,请直接写出对称中心坐标;如成轴对称,请直接写出对称轴的函数关系式.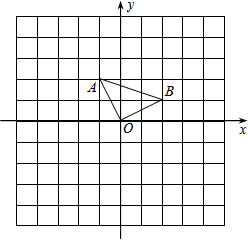
 ,求DE的长.
,求DE的长.

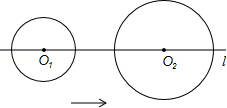
 cm
cm