题目内容
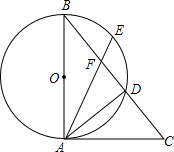
如图,AB是⊙O的直径,点E是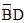 上一点,∠DAC=∠AED.
上一点,∠DAC=∠AED.
(1)求证:AC是⊙O的切线;
(2) 若点E是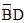 的中点,连结AE交BC于点F,当BD=5, CD=4时,求DF的值.
的中点,连结AE交BC于点F,当BD=5, CD=4时,求DF的值.
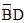 上一点,∠DAC=∠AED.
上一点,∠DAC=∠AED.(1)求证:AC是⊙O的切线;
(2) 若点E是
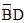 的中点,连结AE交BC于点F,当BD=5, CD=4时,求DF的值.
的中点,连结AE交BC于点F,当BD=5, CD=4时,求DF的值.
(1)证明见解析;(2)2.
试题分析:(1)证明
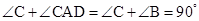 ,可得∠BAC=∠ADC=90°,继而可判断AC是⊙O的切线.
,可得∠BAC=∠ADC=90°,继而可判断AC是⊙O的切线.(2)由△ADC∽△BAC可求得AC=6,由点E是
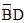 的中点,证明△CAE是等腰三角形,即CA=CF=6,从而求得DF的值.
的中点,证明△CAE是等腰三角形,即CA=CF=6,从而求得DF的值.(1)∵AB是⊙O的直径,
∴∠ADB=∠ADC=90°.
∵∠B=∠AED =∠CAD,∠C=∠C,
∴
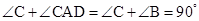 .
.∴∠BAC=∠ADC=90°.
∴AC是⊙O的切线.
(2)可证△ADC∽△BAC.
∴
 ,即AC2=BC×CD=36.解得 AC=6.
,即AC2=BC×CD=36.解得 AC=6.∵点E是
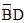 的中点,
的中点,∴∠DAE=∠BAE.
∵∠CAF=∠CAD+∠DAE=∠ABF+∠BAE=∠AFD,
∴CA=CF=6,
∴DF=CA﹣CD=2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
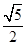 ,求AB的长.
,求AB的长.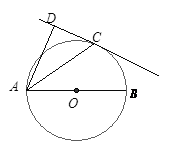
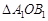 .
.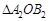 ,并判断
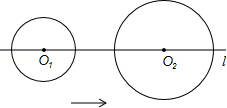
,并判断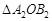 在位置上有何关系?若成中心对称,请直接写出对称中心坐标;如成轴对称,请直接写出对称轴的函数关系式.
在位置上有何关系?若成中心对称,请直接写出对称中心坐标;如成轴对称,请直接写出对称轴的函数关系式.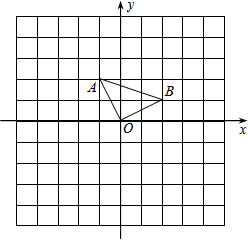
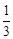 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为