题目内容
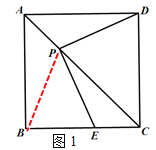
【题目】如图,在正方形ABCD中,P是对角线AC上一点(不与点A、C重合),连接PD,过点P作PE⊥PD交射线BC于点E.
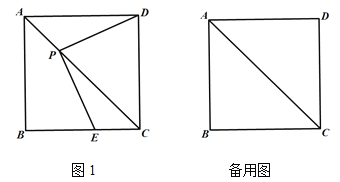
(1)如图1,求证:PD=PE;
(2)若正方形ABCD的边长为4,![]() ,求CE长.
,求CE长.
【答案】(1)证明见解析;(2)2.
【解析】
(1)如图1中,连接PB,利用△APB≌△APD推出PB=PD,再证明PB=PE即可解决问题.
(2)可通过构建等腰直角三角形来求解.过点P作GF∥AB,分别交AD、BC于G、F,那么△AGP和△PFC都是等腰直角三角形,四边形ABFG和四边形GFCD都是矩形,可得AG=BF=PG=1.而PB=PE,PF⊥BE,那么根据等腰三角形三线合一的特点可得出BF=FE=AG=PG,从而CE=BC-2AG=4-2=2.
1)如图1中,连接PB.
∵四边形ABCD是正方形,
∴AB=AD,∠BAC=∠DAC=45°,∠ABC=∠ADC=∠BCD=90°
在△APB和△APD中,
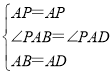 ,
,
∴△APB≌△APD,
∴PB=PD,∠ADP=∠ABP,
∴∠PBC=∠PDC,
∵∠DPE=∠BCD=90°,
∴∠PEC+∠PDC=180°,∠PEB+∠PEC=180°,
∴∠PEB=∠PDC,
∴∠PBC=∠PEB,
∴PB=PE,
∴PD=PE.
(2)过点P作GF∥AB,分别交AD、BC于G、F.如图所示.
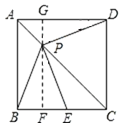
∵四边形ABCD是正方形,
∴四边形ABFG和四边形GFCD都是矩形,
△AGP和△PFC都是等腰直角三角形.
又∵AP=![]() ,AD=4,
,AD=4,
∴GP=AG=BF=1,GD=FC=FP=41=3,
又∵PB=PE,PF⊥BE
∴BF=FE,
∴CE=4-2=2.

【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减(辆) | -1 | +3 | -2 | -4 | +7 | -5 | -10 |
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?