题目内容
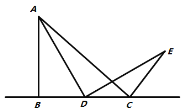
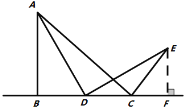
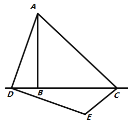
【题目】如图,在△ABC中,AB=AC,点D在△ABC内,BD=BC,∠DBC=60°,点E在△ABC外,∠BCE=150°,∠ABE=60°.
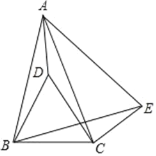
(1)求证:△ADB≌△ADC , 并求出∠ADB的度数;
(2)小明说△ABE是等腰三角形,小华说△ABE是等边三角形.请问 说法更准确,并说明理由.
(3)连接DE,若DE⊥BD,DE=8,求AD的长.
【答案】(1)150°;(2) 小华更准确,理由详见解析;(3)4
【解析】
(1)首先证明△DBC是等边三角形,推出∠BDC=60°,可证明△ADB≌△ADC,继而推出∠ADB=∠ADC即可解决问题;
(2)小华更准确,△ABE是等边三角形.只要证明△ABD≌△EBC即可.
(3)首先证明△DEC是含有30度角的直角三角形,求出EC的长,理由全等三角形的性质即可解决问题.
(1)∵BD=BC,∠DBC=60° ,
∴△DBC是等边三角形 ,
∴DB=DC,∠BDC=∠DBC=∠DCB=60°
在△ADB和△ADC中, 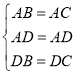 ,
,
∴△ADB≌△ADC(SSS),
∴∠ADB=∠ADC
∴∠ADB=![]() (360°﹣60°)=150°
(360°﹣60°)=150°
(2)解:结论:小华更准确,
理由:
∵∠ABE=∠DBC=60°,
∴∠ABD=∠CBE ,
在△ABD和△EBC中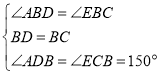 ,
,
∴△ABD≌△EBC(ASA),
∴AB=BE ,
∵∠ABE=60° ,
∴△ABE是等边三角形.
(3)连接DE,
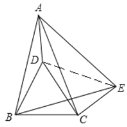
∵∠BCE=150°,∠DCB=60° ,
∴∠DCE=90°,
∵∠EDB=90°,∠BDC=60° ,
∴∠ED=30° ,
∴![]() ,
,
∵△ABD≌△EBC,
∴![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某市为支援灾区建设,计划向![]() 、
、![]() 两受灾地运送急需物资分别为60吨和140吨,该市甲、乙两地有急需物资分别为120吨和80吨,已知甲、乙两地运到
两受灾地运送急需物资分别为60吨和140吨,该市甲、乙两地有急需物资分别为120吨和80吨,已知甲、乙两地运到![]() 、
、![]() 两地的每吨物资的运费如表所示:
两地的每吨物资的运费如表所示:
甲 | 乙 | |
| 20元/吨 | 15元/吨 |
| 25元/吨 | 24元/吨 |
(1)设甲地运到![]() 地的急需物资为
地的急需物资为![]() 吨,求总运费
吨,求总运费![]() (元)关于
(元)关于![]() (吨)的函数关系式,并写出
(吨)的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)求最低总运费,并说明总运费最低时的运送方案.