Question

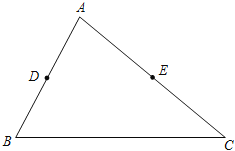
【题目】如图，分别以Rt△ABC的直角边AC、BC为边，在Rt△ABC外作两个等边三角形△ACE和△BCF，连接BE、AF分别交AC、BC边于H、D两点．下列结论：①AF＝BE；②∠AFC＝∠EBC；③∠FAE＝90°；④BD＝FD，其中正确结论的个数是（　　）

A.4个B.3个C.2个D.1个

Answer 1

【答案】C

【解析】

由等边三角形的性质得出BC=CF，CE=AC，∠BCF=∠ACE=∠CFB=∠CBF=∠CAE=60°，∠ACB=90°，易证∠BCE=∠FCA=150°，由SAS证得△BCE≌△FCA，得出AF=BE，∠AFC=∠EBC，由∠FCA=150°，得出∠FAC＜30°，则∠FAE=∠FAC+∠CAE＜90°，由∠BFD＜∠BFC，得出∠BFD＜∠CBF，则DF＞BD，即可得出结果．

∵△ACE和△BCF是等边三角形，

∴BC=CF，CE=AC，∠BCF=∠ACE=∠CFB=∠CBF=∠CAE=60°，∠ACB=90°，

∴∠BCE=90°+60°=150°，∠FCA=60°+90°=150°，

∴∠BCE=∠FCA．

在△BCE和△FCA中，∵，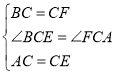

∴△BCE≌△FCA（SAS），

∴AF=BE，∠AFC=∠EBC，故①、②正确；

∵∠FCA=60°+90°=150°，∴∠FAC＜30°．

∵∠CAE=60°，∴∠FAE=∠FAC+∠CAE＜90°，故③错误；

∵∠BFD＜∠BFC，∴∠BFD＜∠CBF，∴DF＞BD，故④错误．

故选：C．