题目内容
【题目】在平面直角坐标系xOy中,将点P沿着y轴翻折,得到的对应点再沿着直线l翻折得到点P1,则P1称为点P的“l变换点”.
(1)已知:点P(1,0),直线l:x=2,求点P的“l变换点”的坐标;
(2)若点Q和它的“l变换点”Q1的坐标分别为(2,1)和(3,2),求直线l的解析式;
(3)如图,⊙O的半径为2.
①若⊙O上存在点M,点M的“l变换点”M1在射线![]() x(x≥0)上,直线l:x=b,求b的取值范围;
x(x≥0)上,直线l:x=b,求b的取值范围;
②将⊙O在x轴上移动得到⊙E,若⊙E上存在点N,使得点N的“l变换点”N1在y轴上,且直线l的解析式为y=![]() x+1,求E点横坐标的取值范围.
x+1,求E点横坐标的取值范围.

【答案】(1)(5,0);(2)y=﹣5x+4;(3)①﹣1≤b≤2;②![]() ﹣4≤t≤
﹣4≤t≤![]() +4.
+4.
【解析】
(1)根据“l变换点”的定义,分别画出图形,即可解决问题;
(2)根据“l变换点”的定义,得到对称点的坐标,根据待定系数法即可得到结论;
(3)①根据“l变换点”的定义,画出图形,求出b的最大值以及最小值即可解决问题;
②如图6中,设点E关于y轴的对称点为E1,E1关于直线y=![]() x+1的对称点为E′,易知当点N在⊙E上运动时,点N′在⊙E′上运动,由此可见当⊙E′与y轴相切或相交时满足条件,想办法求出点E′的坐标即可解决问题.
x+1的对称点为E′,易知当点N在⊙E上运动时,点N′在⊙E′上运动,由此可见当⊙E′与y轴相切或相交时满足条件,想办法求出点E′的坐标即可解决问题.
解:(1)如图1,点P(1,0)关于y轴的对称点(﹣1,0),再关于直线x=2的对称点P1(5,0);
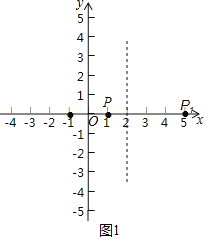
(2)点Q(2,1)关于y轴的对称点(﹣2,1),
设过点(﹣2,1)和(3,2)的直线的解析式为y=kx+b,
![]() ,
,
解得
k=﹣![]() ,b=
,b=![]() ,
,
∴y=﹣![]() x+
x+![]() ,
,
∵点(﹣2,1)和(3,2)关于直线l对称,
∴直线l过点(﹣2,1)和(3,2)连线的中点且与直线y=![]() x+
x+![]() 垂直,
垂直,
∵点(﹣2,1)和(3,2)连线的中点为(![]() ,
,![]() ),
),
∴设直线l的解析式为y=﹣5x+n,
∴![]() =﹣5×
=﹣5×![]() +n,
+n,
解得:n=4,
∴直线l的解析式为:y=﹣5x+4;
(3)①如图4中,
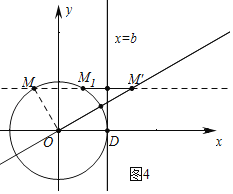
由题意b=![]() M1M′,由此可知,当M1M′的值最大时,可得b的最大值,
M1M′,由此可知,当M1M′的值最大时,可得b的最大值,
∵直线OM′的解析式为y=![]() x,
x,
∴tan∠M′OD=![]() ,
,
∴∠MM′O=∠M′OD=30°,
∵OM=2,易知,OM⊥OM′时,MM′的值最大,最大值为4,
∴b的最大值为2,
如图5中,易知当点M在x轴的正半轴上时,可得b的最小值,最小值为﹣1,
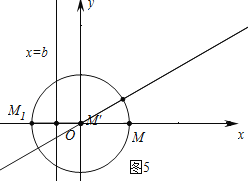
综上所述,满足条件的b取值范围为﹣1≤b≤2;
②设E(t,0),如图6中,设点E关于y轴的对称点为E1,E1关于直线y=![]() x+1的对称点为E′,易知当点N在⊙E上运动时,点N′在⊙E′上运动,由此可见当⊙E′与y轴相切或相交时满足条件.
x+1的对称点为E′,易知当点N在⊙E上运动时,点N′在⊙E′上运动,由此可见当⊙E′与y轴相切或相交时满足条件.
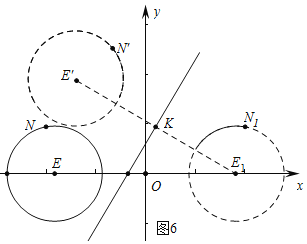
连接E1E′交直线y=![]() x+1于K,易知直线E1E′的解析式为y=﹣
x+1于K,易知直线E1E′的解析式为y=﹣![]() x﹣
x﹣![]() ,
,
由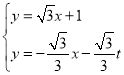 ,解得
,解得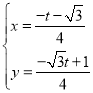 ,
,
∴K(![]() ,
,![]() ),
),
∵KE1=KE′,
∴E′(![]() ,
,![]() ),
),
当⊙E′与y轴相切时,|![]() |=2,解得t=
|=2,解得t=![]() ﹣4或
﹣4或![]() +4,
+4,
综上所述,满足条件的t的取值范围为![]() ﹣4≤t≤
﹣4≤t≤![]() +4.
+4.