题目内容
【题目】在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,把△ABD沿AD折叠后,使得点B落在点E处,连接CE,若∠DBE=15°,则∠ADC的度数为________
【答案】75°或105°
【解析】
分点E落在直线BC上方和下方两种情况进行讨论求解.
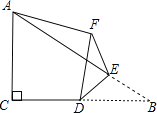
解:当点E在直线BC下方时,如图1所示:
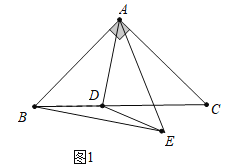
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
根据折叠的性质,可知△ADB≌△ADE,
∴ BD=DE,∠ABD=∠AED=45°,∠DAB=∠DAE,
∴ ∠DBE=∠DEB=15°,
∴∠ABE=∠AEB=∠ABC+∠DBE=45°+15°=60°,
∴∠DAB=![]() (180°-∠ABE -∠AEB)=
(180°-∠ABE -∠AEB)=![]() (180°-60°-60°)=30°,
(180°-60°-60°)=30°,
∴∠ADC=∠ABC+∠DAB =45°+30°=75°.
当点E在直线BC上方时,如图2所示:
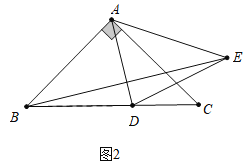
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
根据折叠的性质,可知△ADB≌△ADE,
∴ BD=DE,∠ABD=∠AED=45°,∠DAB=∠DAE,
∴ ∠DBE=∠DEB=15°,
∴∠ABE=∠AEB=∠ABC-∠DBE=45°-15°=30°,
∴∠DAB=![]() (180°-∠ABE -∠AEB)=
(180°-∠ABE -∠AEB)=![]() (180°-30°-30°)=60°,
(180°-30°-30°)=60°,
∴∠ADC=∠ABC+∠DAB =45°+60°=105°.
故答案为:75°或105°.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目