题目内容
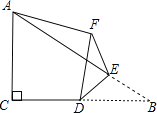
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE,使点B落在点F处,连接AF,则当线段AF的长取最小值时,tan∠FBD是____.
【答案】![]() .
.
【解析】
由题意得:DF=DB,得到点F在以D为圆心,BD为半径的圆上,作⊙D; 连接AD交⊙D于点F,此时AF值最小,由点D是边BC的中点,得到CD=BD=3;而AC=4,由勾股定理得到AD=5,求得线段AF长的最小值是2,连接BF,过F作FH⊥BC于H,根据相似三角形的性质即可得到结论.
由题意得:DF=DB,
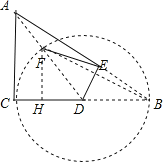
∴点F在以D为圆心,BD为半径的圆上,作⊙D; 连接AD交⊙D于点F,此时AF值最小,
∵点D是边BC的中点,
∴CD=BD=3;而AC=4,
由勾股定理得:AD2=AC2+CD2
∴AD=5,而FD=3,
∴FA=5-3=2,即线段AF长的最小值是2,
连接BF,过F作FH⊥BC于H,
∵∠ACB=90°,
∴FH∥AC,
∴△DFH∽△ADC,
∴![]() ,即
,即![]()
∴HF=![]() ,DH=
,DH=![]() ,
,
∴BH=![]() ,
,
∴tan∠FBD=![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目