题目内容
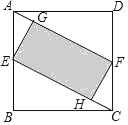
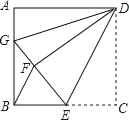
【题目】如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出下列结论:①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
根据正方形的性质和折叠的性质可得AD=DF,∠A=∠GFD=90°,于是根据“HL”判定Rt△ADG≌Rt△FDG,再由GF+GB=GA+GB=12,EB=EF,△BGE为直角三角形,可通过勾股定理列方程求出AG=4,BG=8,进而求出△BEF的面积,再由△BEF是等腰三角形,而△GED显然不是等腰三角形,判断③是错误的,即可得答案.
如图,由折叠可知,DF=DC=DA,∠DFE=∠C=90°,
∴∠DFG=∠A=90°,
在Rt△ADG和Rt△FDG中,
![]() ,
,
∴Rt△ADG≌Rt△FDG,故①正确;
∵正方形边长是12,
∴BE=EC=EF=6,
设AG=FG=x,则EG=x+6,BG=12﹣x,
由勾股定理得:EG2=BE2+BG2,
即:(x+6)2=62+(12﹣x)2,
解得:x=4
∴AG=GF=4,BG=8,BG=2AG,故②正确;
BE=EF=6,△BEF是等腰三角形,易知△GED不是等腰三角形,故③错误;
∵S△GBE=![]() ×6×8=24,S△BEF:S△BGE=EF:EG,
×6×8=24,S△BEF:S△BGE=EF:EG,
∴S△BEF=![]() ×24=
×24=![]() ,
,
故④正确.
综上可知正确的结论是3个.
故选C.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目