题目内容
【题目】已知一次函数y1=kx+b与函数y=﹣2x的图象平行,且与x轴的交点A的横坐标为2.
(1)求一次函数y1=kx+b的表达式;
(2)在给定的网格中,画出函数一次函数y2=x+1的图象,并求出一次函数y1=kx+b与y=x+1图象的交点坐标;
(3)根据图象直接写出,当x取何值时,y1>y2.
【答案】(1)y=-2x+4;(2)交点(1,2),x<1
【解析】试题分析:
(1)由题意可知![]() ,再代入点A的坐标(2,0)解得b的值,即可得到一次函数y1=kx+b的表达式;
,再代入点A的坐标(2,0)解得b的值,即可得到一次函数y1=kx+b的表达式;
(2)由两个一次函数的解析式组成二元一次方程组,解方程组即可求得两函数图象的交点坐标;
(3)根据图象找到![]() 的图象在
的图象在![]() 图象上方部分所对应的自变量的取值范围即可;
图象上方部分所对应的自变量的取值范围即可;
试题解析:
(1)∵一次函数y1=kx+b与函数y=﹣2x的图象平行,
∴![]() ,
,
又∵点A(2,0)在![]() 的图象上,
的图象上,
∴![]() ,解得:b=4,
,解得:b=4,
∴![]() ;
;
(2)画y2=x+1的图象如下图,
解方程组: ![]() 得:
得: ![]() ,
,
∴一次函数![]() 与
与![]() 的交点坐标为(1,2);
的交点坐标为(1,2);
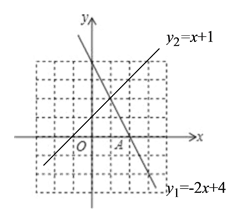
(3)如上图,当![]() 时,
时, ![]() .
.

练习册系列答案
相关题目