题目内容
【题目】如图,A、B分别是x轴上位于原点左右两侧的两点,点P(2,p)在第一象限内,直线PA交y轴与点C(0,2),直线PB交y轴与点D,且S△AOP=4,
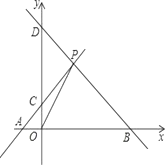
(1)求S△COP;
(2)求点A的坐标及p的值;
(3)若3S△AOP=S△BOP,求直线BD的解析式.
【答案】(1)S△COP=2;
(2)点A的坐标(-2,0),p=4;
(3)直线BD的解析式y=-x+6.
【解析】试题分析:
(1)由已知易得:OC=2,过点P作PE⊥y轴于点E,由点P的横坐标为2,可知PE=2,由此即可计算出△COP的面积;
(2)由(1)中所求的△COP的面积和已知的△AOP的面积可求得△AOC的面积,结合OC=2可求得OA的长,从而可得点A的坐标;利用S△AOP=![]() OA·p=4即可解得p的值;
OA·p=4即可解得p的值;
(3)先由3S△AOP=S△BOP=12=![]() OB·p结合(2)中求得的p的值解出OB的值,即可得到点B的坐标,然后由点P、B的坐标用“待定系数法”即可求得BD的解析式.
OB·p结合(2)中求得的p的值解出OB的值,即可得到点B的坐标,然后由点P、B的坐标用“待定系数法”即可求得BD的解析式.
试题解析:
(1)如图,过点P作PE⊥y轴于点E,
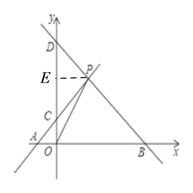
∵点P的横坐标为2,点C的坐标为(0,2),
∴PE=2,OC=2,
∴S△COP=![]() OC·PE=
OC·PE=![]() .
.
(2)∵S△COP=2,S△AOP=4,
∴S△AOC=4-2=2,
又∵S△AOC=![]() OA·OC,OC=2,
OA·OC,OC=2,
∴OA=2,
∴点A的坐标为(-2,0);
∵S△AOP=![]() OA·p=4,
OA·p=4,
∴![]() ,解得:p=4.
,解得:p=4.
(3)∵3S△AOP=S△BOP,S△BOP=![]() OB·p,S△AOP=4,p=4,
OB·p,S△AOP=4,p=4,
∴![]() OB×4=12,解得:OB=6,
OB×4=12,解得:OB=6,
∴点B的坐标为(6,0).
设直线BD的解析式为:y=kx+b,代入点P(2,4)和点B(6,0)可得:
![]() ,解得:
,解得: ![]() ,
,
∴直线BD的解析式y=-x+6.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目