题目内容
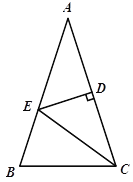
【题目】如图,在平行四边形ABCD中,∠DAB=60°,AB=2AD,点 E、F分别是AB、CD的中点,过点A作AG∥BD,交CB的延长线于点G.
(1)求证:四边形DEBF是菱形;
(2)请判断四边形AGBD是什么特殊四边形?并加以证明.

【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD且AB=CD,AD∥BC且AD=BC.
E,F分别为AB,CD的中点,
∴BE=![]() AB,DF=
AB,DF=![]() CD,
CD,
∴BE=BF,
∴四边形DEBF是平行四边形
在△ABD中,E是AB的中点,
∴AE=BE=![]() AB=AD,
AB=AD,
而∠DAB=60°,
∴△AED是等边三角形,即DE=AE=AD,
故DE=BE.
∴平行四边形DEBF是菱形.
(2)解:四边形AGBD是矩形,理由如下:
∵AD∥BC且AG∥DB,
∴四边形AGBD是平行四边形.
由(1)的证明知AD=DE=AE=BE,
∴∠ADE=∠DEA=60°,
∠EDB=∠DBE=30°.
故∠ADB=90°.
∴平行四边形AGBD是矩形.
【解析】(1)利用平行四边形的性质证得△AED是等边三角形,从而证得DE=BE,问题得证;
(2)利用平行四边形的性质证得∠ADB=90°,利用有一个角是直角的平行四边形是矩形判定矩形.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目