题目内容
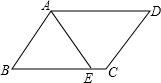
已知：如图，在?ABCD中，E、F是对角线AC上的两点，且AE=CF．
求证：∠ADF=∠CBE．
求证：∠ADF=∠CBE．
证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=CB．
∴∠DAF=∠BCE．
∵AE=CF，
∴AE+EF=CF+EF．
∴AF=CE．
在△ADF和△CBE中，
，
∴△ADF≌△CBE．
∴∠ADF=∠CBE．
∴AD∥BC，AD=CB．
∴∠DAF=∠BCE．
∵AE=CF，
∴AE+EF=CF+EF．
∴AF=CE．
在△ADF和△CBE中，
|
∴△ADF≌△CBE．
∴∠ADF=∠CBE．
练习册系列答案
阅读快车系列答案
相关题目
Q从点C出发，沿CB向点B运动，P、Q的运动速度均为1cm/s，两点中有一点到达目的地时，另一点也停止运动，