Question

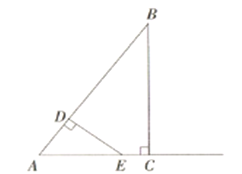
【题目】如图，抛物线与轴交于点和点，对称轴分别交抛物线和轴于点和点，以为底边向上作等腰．

（1）______；______（用含的代数式表示）；

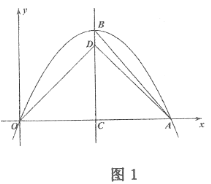
（2）如图1，当时，连接，求的值；

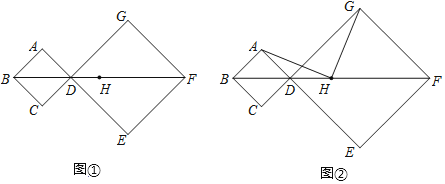
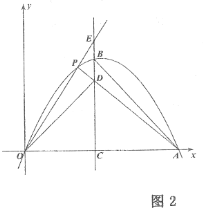
（3）点是抛物线段上任意一点，连接和，延长交对称轴于点，如图2，若，，三点在一条直线上，当时，求的值．

Answer 1

【答案】（1）4；-8a；（2）；（3）．

【解析】

（1）根据等腰直角三角形的性质可求出CD的长，由点A的坐标，利用待定系数法可用含的代数式表示出值；

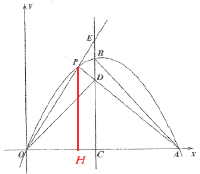
（2）代入可求出抛物线的解析式，利用配方法可求出点B的坐标，进而可得出BC的长度，结合CD的长可求出BD的长，由△BDA和△CDA等高，可得出 ，代入BD，CD的值即可求出结论； （3）过点作轴于点，由OC，CD的长可得出点D的坐标，由点A，D的坐标， 可得，可得PH＝AH，再利用，表示出OP，OE之间数量关系，利用相似三角形的性质求出OH的值，可得P的坐标，即可得到答案．

（1）：

（2）当时，则二次函数表达式为，

故可得点的坐标为，则，

故

（3）过点作轴于点，由，，三点共线可知，，则有，设，则；又因为，所以，即；又易证，故，解得，所以点坐标为，代入得：．