题目内容
【题目】如图,把一个量角器与一块30°(∠CAB=30°)角的三角板拼在一起,三角板的斜边AB与量角器所在圆的直径MN重合,现有射线CP绕点C从CA开始沿顺时针方向以每秒2°的速度旋转到与CB重合,就停止旋转.在旋转过程中,射线CP与量角器的半圆弧交于E.连接BE.
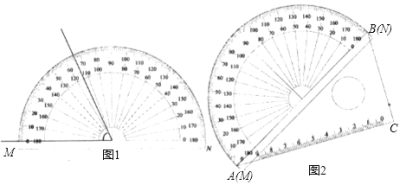
(1)设旋转x秒后,点E处的读数为y°,则y与x的函数关系式________.
(2)当CP旋转________秒时,△BCE是等腰三角形.
【答案】(1)y=4x(0≤x≤45);(2)7.5或30
【解析】
(1)由题意∠ACE=2x°,∠AOE=y°,根据圆周角定理可知∠AOE=2∠ACE,可得y=4x(0≤x≤45);
(2)分两种情形分别讨论求解即可,①如图,当BE=EC时,则有EO垂直平分BC,先根据平行线的性质求出∠AOE=∠BAC=30°,再利用圆周角定理得出∠ACE的度数,从而可得出结果;②当BC=BE时,则有OB垂直平分EC,先判定△BOE是等边三角形,再求出∠AOE的度数,再利用圆周角定理得出∠ACE的度数,从而可得出结果.
解:(1)如图,由题意知∠ACE=2x°,∠AOE=y°,
又∠ACB=90°,∴点C在以O为圆心,AB为直径的圆上,
又MN=AB,∴点C也在以MN为直径的圆上,
∴∠AOE=2∠ACE=4x°,
故答案为:y=4x(0≤x≤45);
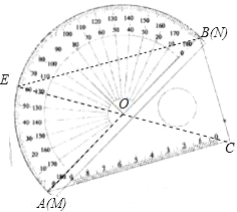
(2)①如图,当BE=EC时,
连接OC,则OB=OC,又EB=EC,
∴EO垂直平分BC,

∵AC⊥BC,∴EO∥AC,
∴∠AOE=∠BAC=30°,
∴∠ACE=![]() ∠AOE=15°,
∠AOE=15°,
t=15÷2=7.5(秒).
②如图,当BC=BE时,
连接OC,则OE=OC,又BC=BE,
∴OB垂直平分EC,
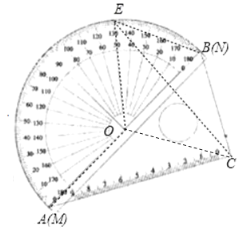
∴∠OBE=∠OBC=60°,
又OE=OB,
∴△BOE是等边三角形,
∴∠AOE=120°,
∴∠ACE=![]() ∠AOE=60°,
∠AOE=60°,
∴t=60÷2=30(秒).
综上可知,当CP旋转7.5秒或30秒时,△BCE是等腰三角形.
故答案为:7.5或30.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案