题目内容
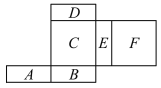
【题目】如图，在正方形ABCD中，E为CD边上一点，F为BC延长线上一点，CE=CF，∠FDC=30°，求∠BEF的度数．
【答案】∠BEF=105°．
【解析】试题分析：根据正方形的性质得出∠BCD=∠DCF=90°，BC=CD，结合已知条件得出△BCE和△DCF全等，从而得出∠EBC=∠FDC=30°，即∠BEC=60°，根据等腰直角三角形得出∠FEC=45°，从而得出∠BEF的度数．
试题解析：解：∵四边形ABCD是正方形，∴∠BCD=∠DCF=90°，BC=CD，
∵CE=CF，∠FDC=30°，∴△BCE≌△DCF， ∴∠EBC=∠FDC=30°，
∴∠BEC=60°， ∵∠DCF=90°，CE=CF， ∴∠FEC=45°，
∴∠BEF=∠BEC+∠FEC=60°+45°=105°．
练习册系列答案
相关题目
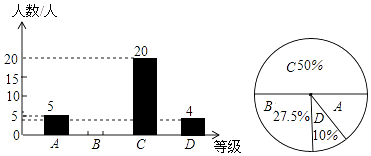
【题目】课题小组从某市20000名九年级男生中，随机抽取了1000名进行50米跑测试，并根据测试结果绘制了如下尚不完整的统计图表．
等级 | 人数/名 |
优秀 | a |
良好 | b |
及格 | 150 |
不及格 | 50 |
解答下列问题：
（1）a等于多少？，b等于多少？
（2）补全条形统计图；
（3）试估计这20000名九年级男生中50米跑达到良好和优秀等级的总人数．
