题目内容
【题目】如图,在△ABC中,AB=AC,∠BAC=60°.在△ABC的外侧作直线AP,点C关于直线AP的对称点为D,连接AD,BD.
(1)依据题意补全图形;
(2)当∠PAC等于多少度时,AD∥BC?请说明理由;
(3)若BD交直线AP于点E,连接CE,求∠CED的度数;
(4)探索:线段CE,AE和BE之间的数量关系,并说明理由.

【答案】(1)详见解析;(2)30°;(3)120(4)![]()
【解析】
(1)根据题意画出图形即可;
(2)连接CD,交AP于CD于F,因为AD∥BC,所以∠C=∠CAD,由对称可得AC=AD,CF=FD,AF⊥CD,所以AP平分∠CAD,即可求解.
(3)AD=AC,∠DAP=∠CAP,∠DEP=∠PEC,求出AB=AC=AD,得到∠ABE=∠D,在△ABE中,得∠ABE+∠AEB+∠BAE=180°,得到∠D+∠CAE+60°+∠D+∠CAE =180°,求出∠D+∠CAE=60°,证明∠DEP=60°,即可求解;
(4)CE +AE=BE,如图,在BE上取点M使ME=AE,连接AM,设∠EAC=∠DAE=x,求得∠AEB=60°,从而得到△AME为等边三角形,根据等边三角形的性质和SAS即可判定△AEC≌△AMB,根据全等三角形的性质可得CE=BM,由此即可证得CE+AE=BE.
(1)
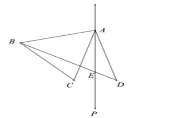
(2)连接CD,交AP于F,

∵AB=AC,∠BAC=60°
∴等边三角形ABC
∴∠BCA=60°
∵AD∥BC
∴∠BCA=60°=∠DAC
由对称可得AC=AD,CF=FD,AF⊥CD
∴AP平分∠CAD
∴∠PAC=30°
(3)由对称可得AD=AC,∠DAE=∠CAE,∠DEP=∠PEC
∵等边三角形ABC
∴AB=AC=AD
∴∠ABE=∠D
∵△ABE
∴∠ABE+∠AEB+∠BAE=180°
∴∠ABE+∠AEB+∠BAC+∠CAE=180°
∴∠D+∠CAE+60°+∠D+∠CAE =180°
∴∠D+∠CAE=60°
∴∠DEP=60°
∴∠DEC=120°;

(4)CE+AE=BE.
在BE上取点M使ME=AE,连接AM,
在等边△ABC中,
AC=AB,∠BAC=60°
由对称可知:AC=AD,∠EAC=∠EAD,
设∠EAC=∠DAE=x.
∵AD=AC=AB,
∴∠D=60°-x
∴∠AEB=60-x+x=60°.
∴△AME为等边三角形.
∴AM=AE,∠MAE=60°,
∴∠BAC=∠MAE=60°,
即可得∠BAM=∠CAE.
在△AMB和△AEC中,AB=AC,∠BAM=∠CAE, AM=AE,
∴△AMB≌△AEC.
∴CE=BM.
∴CE+AE=BE.









