题目内容
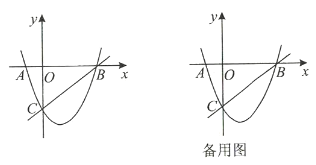
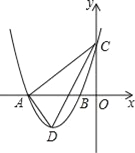
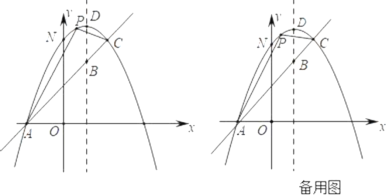
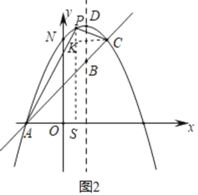
【题目】如图，已知抛物线y＝﹣x2+bx+c与一直线相交于A（﹣1，0），C（2，3）两点，与y轴交于点N，其顶点为D．
（1）求抛物线及直线AC的函数关系式；
（2）若P是抛物线上位于直线AC上方的一个动点，设点P的横坐标为t；
①当S△ACP＝S△ACN时，求点P的坐标；
②是否存在点P，使得△ACP是以AC为斜边的直角三角形？若存在，求点P的坐标；若不存在，请说明理由；
（3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF∥BD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，请直接写出点E的坐标；若不能，请说明理由．
【答案】（1）抛物线解析式为y＝﹣x2+2x+3，直线AC解析式为y＝x+1；（2）①P（1，4），②P（
，
）；（3）点E的坐标为：（0，1）或（
，
）或（
，
）
【解析】
（1）设直线AC的解析式为y=mx+n，根据二次函数和一次函数图象上点的坐标特征，利用待定系数法求出b、c，m、n的值，即可得答案；（2）①根据二次函数解析式可得N点坐标，过点N作NP//AC，根据平行线间的距离相等可得S△ACP＝S△CAN，设直线NP的解析式为y=kx+a，由NP//AC可得k=1，把N点坐标代入可得a=3，可得直线NP的解析式，联立直线NP与二次函数解析式即可得P点坐标；②过P作PS⊥x轴于S，过C作CK⊥PS于K，则∠CKP＝∠PSA＝90°，根据点A、C、P、的坐标可用t表示出CK、PK、PS和AS的长，根据直角三角形两锐角的互余关系可得∠APS＝∠PCK，即可证明△APS∽△PCK，根据相似三角形的性质列方程求出t值即可；（3）把二次函数解析式配方，可得顶点D的坐标，可求出BD的长，设点E（m，m+1），可用m表示点F的坐标，即可表示出EF的长，根据平行四边形的性质可得EF=BD，列方程求出m的值即可得答案.
（1）将A（﹣1，0），C（2，3）代入y＝﹣x2+bx+c中，得
，
解得：
，
∴抛物线解析式为y＝﹣x2+2x+3，
设直线AC解析式为y＝mx+n，
∵点A（-1，0）、C（2，3）在直线AC上，
∴
，
解得：
，
∴直线AC解析式为y＝x+1.
（2）①在y＝﹣x2+2x+3中，令x＝0，得y＝3，
∴N（0，3），
∵点P的横坐标为t，点P在抛物线y=-x2+2x+3图象上，
∴P（t，﹣t2+2t+3），
如图，过点P作PH//AC，
∵平行线间的距离相等，
∴S△ACP＝S△CAN，
设直线NP的解析式为y=kx+a，
∴k=1，
把N（0，3）代入得a=3，
∴直线NP的解析式为y=x+3，
联立直线NP与抛物线解析式得
，
解得：
或
（舍去），
∴P（1，4）.
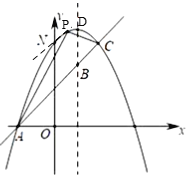
②如图2，过P作PS⊥x轴于S，过C作CK⊥PS于K，则∠CKP＝∠PSA＝90°，
∵P（t，﹣t2+2t+3），A（﹣1，0），C（2，3），
∴CK＝2﹣t，PK＝﹣t2+2t，PS＝﹣t2+2t+3，AS＝t﹣（﹣1）＝t+1，
∵△ACP是以AC为斜边的直角三角形，
∴∠APS+∠CPK＝∠APC＝90°，
∵∠PCK+∠CPK＝90°，
∴∠APS＝∠PCK，
∴△APS∽△PCK，
∴
＝
，即
＝
，
解得：t＝
，
∵P是抛物线上位于直线AC上方的一个动点，
∴﹣1＜t＜2，
∵
＞2，
∴t＝，
∴﹣t2+2t+3=，
∴P（，）．
（3）∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4，
∴顶点D（1，4），
∴B（1，2），BD＝2，
∵点E在直线AC上，AC解析式为y=x+1，
∴设点E（m，m+1），
∵B，D，E，F为顶点的四边形为平行四边形，
∴EF=BD，
∵EF//BD，BD为抛物线对称轴，
∴F（m，﹣m2+2m+3），EF＝
，
∴m2-m-2＝±2，解得：m1＝0，m2＝1（舍去），m3＝，m4＝，
∴，以B，D，E，F为顶点的四边形能为平行四边形，点E的坐标为：（0，1）或（，）或（，）．
