题目内容
【题目】如图,抛物线y1=a(x+2)2-3与y2=![]() (x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=3AC;其中正确结论是( )
(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=3AC;其中正确结论是( )
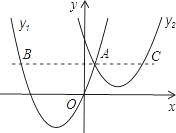
A.①②B.②③C.③④D.①④
【答案】D
【解析】
直接由![]() 判断①;把A点坐标代入抛物线y1=a(x+2)2-3求出a值判断②;由x=0求得y2,y1作差后判断③;由二次函数的对称性求出B,C的坐标,进一步验证2AB=3AC判断④.
判断①;把A点坐标代入抛物线y1=a(x+2)2-3求出a值判断②;由x=0求得y2,y1作差后判断③;由二次函数的对称性求出B,C的坐标,进一步验证2AB=3AC判断④.
解:对于①,![]() ,∴无论x取何值,y2的值总是正数正确;
,∴无论x取何值,y2的值总是正数正确;
对于②,∵抛物线y1=a(x+2)2-3过点A(1,3),则3=a(1+2)2-3,解得![]() ,②错误;
,②错误;
对于③,![]() ,当x=0时,
,当x=0时,![]() ,③错误;
,③错误;
对于④,∵抛物线y1=a(x+2)2-3与![]() 交于点A(1,3),∴可求得B(-5,3),C(5,3),求得AB=6,AC=4,则2AB=3AC,④正确.
交于点A(1,3),∴可求得B(-5,3),C(5,3),求得AB=6,AC=4,则2AB=3AC,④正确.
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目