��Ŀ����
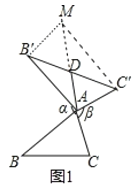
����Ŀ��С���о�������һ�������⣺��ͼ 1����ABC �У��� AB �� A ˳ʱ����ת 00 1800 �õ� AB ���� AC �Ƶ� A ��ʱ����ת �õ� AC ������ BC ���� 180�� ʱ�� ����ABC �� BC �ϵ����� AD �� BC ��������ϵ��ʲô�� �����������о����̣�

������֤��
��1������ͼ 2����ABC Ϊ�ȱ�������ʱ��AD �� BC ��������ϵΪ AD ����BC ��
����ͼ 3����BAC 900 , BC 8ʱ���� AD ��Ϊ ��������
������֤��
��2����ͼ 1 �У���ABC Ϊ����������ʱ������ AD �� BC ��������ϵ��������֤����
��չӦ��
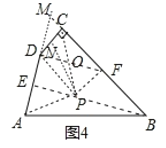
��3����ͼ 4�����ı��� ABCD ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����ı����ڲ��Ƿ���ڵ� P ��ʹPDC ��PAB ֮������С��̽���������еı߽ǹ�ϵ�������ڣ� �뻭���� P ��λ�ã�������ͼ�ۼ�������Ҫ˵������ֱ��д��PDC �ı� DC �ϵ����� PQ �ij��ȣ��������ڣ�˵�����ɣ�
�����ı����ڲ��Ƿ���ڵ� P ��ʹPDC ��PAB ֮������С��̽���������еı߽ǹ�ϵ�������ڣ� �뻭���� P ��λ�ã�������ͼ�ۼ�������Ҫ˵������ֱ��д��PDC �ı� DC �ϵ����� PQ �ij��ȣ��������ڣ�˵�����ɣ�
���𰸡���1����![]() ��4 ��2��
��4 ��2��![]() ��֤�������� ��3�����ڣ���ͼ��������
��֤�������� ��3�����ڣ���ͼ��������![]()
��������
��1��������֤��![]() �Ǻ���30����ֱ�������Σ��ɵ�
�Ǻ���30����ֱ�������Σ��ɵ�![]() �����ɽ�����⣻������֤��
�����ɽ�����⣻������֤��![]() ������ֱ��������б�����߶������ɽ�����⣻
������ֱ��������б�����߶������ɽ�����⣻
��2�����ۣ�![]() ���ӳ�AD��M��ʹ��
���ӳ�AD��M��ʹ��![]() ������
������![]() ����֤���ı���
����֤���ı���![]() ��ƽ���ı��Σ���֤��
��ƽ���ı��Σ���֤��![]() �����ɽ�����⣻
�����ɽ�����⣻
��3�����ڣ���ͼ4���ӳ�AD��BC���ӳ�����M����![]() ��E�����߶�BC�Ĵ�ֱƽ���߽�BE��P����BC��F������PA��PD��PC������PCD������PN������DF��PC��O����֤��
��E�����߶�BC�Ĵ�ֱƽ���߽�BE��P����BC��F������PA��PD��PC������PCD������PN������DF��PC��O����֤��![]() ����֤��
����֤��![]() �����ɵó����ۣ��ٸ��ݹ��ɶ������PC�ij����������PQ�ij���
�����ɵó����ۣ��ٸ��ݹ��ɶ������PC�ij����������PQ�ij���
��1���١ߡ�ABC�ǵȱ�������
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
�ʴ�Ϊ��![]()
�ڡ�![]()
��![]()
��![]()
��![]()
��![]()
��![]()
�ʴ�Ϊ��4��
��2��![]()
��ͼ��1���У��ӳ�AD��M��ʹ��![]() ������
������![]()
��![]()
���ı���![]() ��ƽ���ı���
��ƽ���ı���
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]() ��
��
��3�����ڣ���ͼ4���ӳ�AD��BC���ӳ�����M����![]() ��E�����߶�BC�Ĵ�ֱƽ���߽�BE��P����BC��F������PA��PD��PC������PCD������PN������DF��PC��O
��E�����߶�BC�Ĵ�ֱƽ���߽�BE��P����BC��F������PA��PD��PC������PCD������PN������DF��PC��O
��![]()
��![]()
��![]()
��![]()
��Rr��DCM��
��![]()
��![]()
��Rt��BEM��
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]() ��
��![]()
��Rt��CDF��
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
���ı���CDPF�Ǿ���
��![]()
��![]()
���ADP�ǵȱ�������
��![]()
��![]()
��![]()
��![]()
���ɣ�1�����۵�![]()
��PDC ��PAB ֮������С��̽���������еı߽ǹ�ϵ
��Rt��FCP��
��![]()
��![]()
��![]() ��
��