��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У���A��B������ֱ�ΪA��a��0����B��b��0������a��b����|a+b��2|+ ![]() =0����ͬʱ����A��B�ֱ�����ƽ��1����λ��������ƽ��2����λ���ֱ�õ���A��B�Ķ�Ӧ��ΪC��D��
=0����ͬʱ����A��B�ֱ�����ƽ��1����λ��������ƽ��2����λ���ֱ�õ���A��B�Ķ�Ӧ��ΪC��D�� 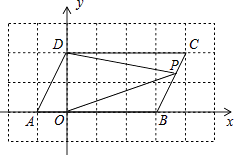
��1����ֱ��д��A��B��C��D�ĵ�����겢������ϵ�л�����A��B��C��D������AC��BD��CD��
��2����E���������ϣ���S��BCE=S�ı���ABDC �� �����������ĵ�E�����꣮
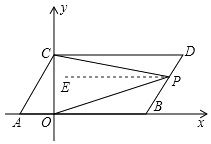
��3����P���߶�BD�ϵ�һ�����㣬����PC��PO������P���߶�BD���ƶ�ʱ������B��D�غϣ�֤���� ![]() �Ǹ�������
�Ǹ�������
���𰸡�
��1���⣺��������ã� ![]() ��
��
��ã�a=��1��b=3��
����A����1��0����B��3��0����C��0��2����D��4��2����
��ͼ��
��2���⣺��AB=3������1��=3+1=4��
��S�ı���ABDC=4��2=8��
��S��BCE=S�ı���ABDC��
��E��y����ʱ����E��0��y����
�� ![]() |y��2|3=8��
|y��2|3=8��
��ã�y=�� ![]() ��y=
��y= ![]() ��
��
�� ![]() ��
��
��E��x����ʱ����E��x��0����
�� ![]() |x��3|2=8��
|x��3|2=8��
��ã�x=11��x=��5��
��E����5��0������11��0��
��3���⣺��ƽ�Ƶ����ʿɵ�AB��CD��
��ͼ������P��PE��AB����PE��CD��
���DCP=��CPE����BOP=��OPE��
���CPO=��CPE+��OPE=��DCP+��BOP��
����DCP+��BOP=��CPO��
���Ա�ֵΪ1
����������1�����ݷǸ������������a��b��ֵ�ó���A��B�����꣬����ƽ�ƿɵõ�C��D�����꣬����֪�𰸣���2���ֵ�E��x���y�������������������꣬����S��BCE=S�ı���ABDC�г��������ɵã���3����PE��AB����PE��CD���ɵá�DCP=��CPE����BOP=��OPE���̶�֪��CPO=��CPE+��OPE=��DCP+��BOP�����ɵô𰸣�