题目内容
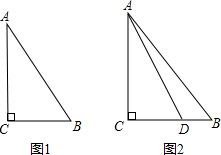
在直角三角形中∠ACB=90°，CD，CE三等分∠ACB，CD⊥AB，求证：AB=2BC．
证明：如图，∵∠ACB=90°，CD，CE三等分∠ACB，
∴∠ACD=60°，
∵CD⊥AB，
∴∠A=30°，
∴AB=2BC．
分析：通过已知条件可以求得∠ACD=60°，则由直角三角形的两个锐角互余的性质得到∠A=30°，所以“30度角所对的直角边等于斜边的一半”．
点评：本题考查了含30度角的直角三角形．在直角三角形中，30°角所对的直角边等于斜边的一半．
∴∠ACD=60°，
∵CD⊥AB，
∴∠A=30°，
∴AB=2BC．
分析：通过已知条件可以求得∠ACD=60°，则由直角三角形的两个锐角互余的性质得到∠A=30°，所以“30度角所对的直角边等于斜边的一半”．
点评：本题考查了含30度角的直角三角形．在直角三角形中，30°角所对的直角边等于斜边的一半．
练习册系列答案
相关题目
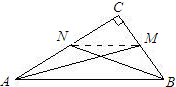求证：在直角三角形中两条直角边上的中线的平方和的4倍等于斜边平方的5倍．如图所示．设直角三角形ABC中，∠C=90°，AM，BN分别是BC，AC边上的中线，且AM2+BN2=AB2+MN2．
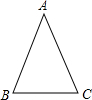通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sadA=
学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，也可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=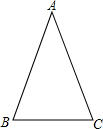
（2014•宝山区一模）通过锐角三角比的学习，我们已经知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长比与角的大小之间可以相互转化．类似的我们可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图在△ABC中，AB=AC，