��Ŀ����
 ѧϰ�����Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת�������Ƶģ�Ҳ�����ڵ����������н����߽�֮�����ϵ�����Ƕ��壺�����������еױ������ıȽ������ǵ����ԣ�sad������ͼ���ڡ�ABC�У�AB=AC������A�����Լ���sadA����ʱsad A=
ѧϰ�����Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת�������Ƶģ�Ҳ�����ڵ����������н����߽�֮�����ϵ�����Ƕ��壺�����������еױ������ıȽ������ǵ����ԣ�sad������ͼ���ڡ�ABC�У�AB=AC������A�����Լ���sadA����ʱsad A=| 1 |
| 2 |
���������Խǵ����Զ��壬���������⣺
��1����գ�sad60��=
1
1
��sad90��=| 2 |
| 2 |
| 3 |
| 3 |
��2������0�㣼A��180�㣬��A������ֵsadA��ȡֵ��Χ��
0��sadA��2
0��sadA��2
����3����ͼ����֪sinA=
| 3 |
| 5 |
��4����sinA=k����ֱ����k�Ĵ���ʽ��ʾsadA��ֵΪ
2-2
|
2-2
|
��������1����A=60�㣬������Ϊ�ȱ������Σ��ױ�������ȣ���A=90�㣬������Ϊ����ֱ�������Σ��ױ�������
������A=120�㣬���ױ��ϵĸߣ���Ϊ30�㣬����õױ�������
����Ȼ����ݵ����������еױ������ıȽ������ǵ����ԣ�sad�����ɵõ��𰸣�
��2��0�㣼A��180�㣬�������������ߵĹ�ϵ�õ�����֮�ʹ��ڵױ��ɵõ�0��sadA��2��
��3����B��BD��AC��D����BD=3x��AB=5x�����ù��ɶ��������AD=4x����DC=x����Rt��BDC�и��ݹ��ɶ������BC��Ȼ����ݶ��ǵ����Զ�����ֵ���ɣ�
��4���루3���ļ��㷽��һ����
| 2 |
| 3 |
��2��0�㣼A��180�㣬�������������ߵĹ�ϵ�õ�����֮�ʹ��ڵױ��ɵõ�0��sadA��2��
��3����B��BD��AC��D����BD=3x��AB=5x�����ù��ɶ��������AD=4x����DC=x����Rt��BDC�и��ݹ��ɶ������BC��Ȼ����ݶ��ǵ����Զ�����ֵ���ɣ�
��4���루3���ļ��㷽��һ����
����⣺��1��1��
��
��
��2��0��sadA��2��
��3����B��BD��AC��D����ͼ��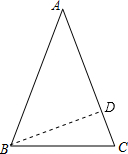
��sinA=
=
��
��BD=3x��AB=5x��
��AD=
=4x��
��DC=5x-4x=x��
��Rt��BDC��BC=
=
=
x��
��sadA=
=
��
��4������ͼ��
sinA=k��BD=kAB��
��AD=
=
AB��
��DC=AC-AD=��1-
��AB��
��BC=
=
AB��
��sadA=
=
��
�ʴ�Ϊ
��
| 2 |
| 3 |
��2��0��sadA��2��
��3����B��BD��AC��D����ͼ��

��sinA=
| 3 |
| 5 |
| BD |
| AB |
��BD=3x��AB=5x��
��AD=
| (5x)2-(3x)2 |
��DC=5x-4x=x��
��Rt��BDC��BC=
| BD2+DC2 |
| (3x)2+x2 |
| 10 |
��sadA=
| BC |
| AB |
| ||
| 5 |
��4������ͼ��
sinA=k��BD=kAB��
��AD=
| AB2-BD2 |
| 1-k2 |
��DC=AC-AD=��1-
| 1-k2 |
��BC=
| BD2+DC2 |
2-2
|
��sadA=
| BC |
| AB |
2-2
|
�ʴ�Ϊ
2-2
|
���������⿼���˽�ֱ�������Σ��������Ǻ����Ķ�����ɶ��������������δ֪�ĽǺͱߣ�

��ϰ��ϵ�д�
�����Ŀ
����С������10�֣�
ѧϰ�����Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת��.
���Ƶģ������ڵ����������н����߽�֮�����ϵ�����Ƕ��壺�����������еױ������ıȽ������ǵ����ԣ�sad��.��ͼ���ڡ�ABC�У�AB=AC������A�����Լ���sadA����ʱsad A=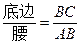 .����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����.
.����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����.
���������Խǵ����Զ��壬���������⣺
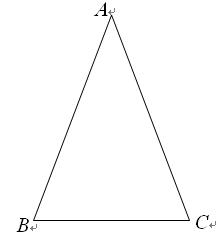
��1��sad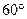 ��ֵΪ�� ��
��ֵΪ�� ��
��2������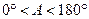 ����A������ֵsad A��ȡֵ��Χ�� .
����A������ֵsad A��ȡֵ��Χ�� .
��3����֪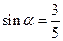 ������
������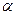 Ϊ��ǣ�����sad
Ϊ��ǣ�����sad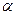 ��ֵ.
��ֵ.
ѧϰ�����Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת��.
���Ƶģ������ڵ����������н����߽�֮�����ϵ�����Ƕ��壺�����������еױ������ıȽ������ǵ����ԣ�sad��.��ͼ���ڡ�ABC�У�AB=AC������A�����Լ���sadA����ʱsad A=
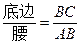 .����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����.
.����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����.���������Խǵ����Զ��壬���������⣺

��1��sad
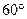 ��ֵΪ�� ��
��ֵΪ�� ��A�� | B��1 | C��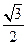 | D��2 |
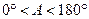 ����A������ֵsad A��ȡֵ��Χ�� .
����A������ֵsad A��ȡֵ��Χ�� .��3����֪
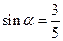 ������
������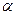 Ϊ��ǣ�����sad
Ϊ��ǣ�����sad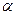 ��ֵ.
��ֵ. ѧϰ�����Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת��.���Ƶģ������ڵ����������н����߽�֮�����ϵ�����Ƕ��壺�����������еױ������ıȽ������ǵ����ԣ�sad��.��ͼ���ڡ�ABC�У�AB=AC������A�����Լ���sadA ����ʱsadA=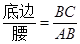 .����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����. �����������ڽǵ����Զ��壬����������⣺
.����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����. �����������ڽǵ����Զ��壬����������⣺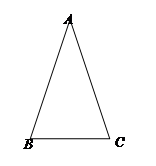
��С��1��sad ��ֵΪ�� �� ��
��ֵΪ�� �� ��
A��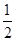 | B��1 | C��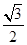 | D��2 |
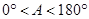 ����A������ֵsadA��ȡֵ��Χ��( �� )
����A������ֵsadA��ȡֵ��Χ��( �� )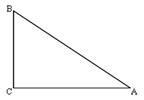
A��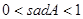 | B��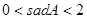 | C��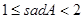 |
D��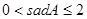 |
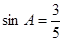 ��AB=25����sadA��ֵ
��AB=25����sadA��ֵ 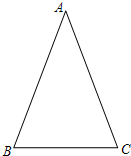 ѧϰ�����Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת����
ѧϰ�����Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת����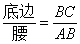 .����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����.
.����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����.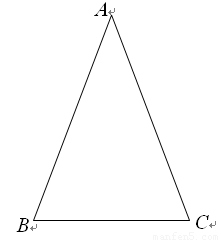
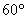 ��ֵΪ�� ��A.
��ֵΪ�� ��A. 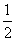 B.
1 C.
B.
1 C. 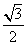 D.
2
D.
2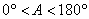 ����A������ֵsad A��ȡֵ��Χ��
.
����A������ֵsad A��ȡֵ��Χ��
.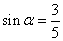 ������
������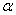 Ϊ��ǣ�����sad
Ϊ��ǣ�����sad