题目内容
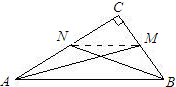 求证:在直角三角形中两条直角边上的中线的平方和的4倍等于斜边平方的5倍.如图所示.设直角三角形ABC中,∠C=90°,AM,BN分别是BC,AC边上的中线,且AM2+BN2=AB2+MN2.
求证:在直角三角形中两条直角边上的中线的平方和的4倍等于斜边平方的5倍.如图所示.设直角三角形ABC中,∠C=90°,AM,BN分别是BC,AC边上的中线,且AM2+BN2=AB2+MN2.求证:4(AM2+BN2)=5AB2.
分析:分析由于AM,BN,AB均可看作某个直角三角形的斜边,可从勾股定理入手.我们分别把M,N当成所在边的中点,那么可直接利用AM2+BN2=AB2+MN2.
解答: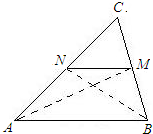 证明:连接MN,线段MN称为△ABC的中位线,
证明:连接MN,线段MN称为△ABC的中位线,
∴MN∥AB且MN=
AB
AM2+BN2=AB2+MN2,
所以4(AM2+BN2)=4AB2+4MN2.
由于M,N是BC,AC的中点,
所以MN=
AB.
所以4MN2=AB2.
∴4(AM2+BN2)=5AB2.
 证明:连接MN,线段MN称为△ABC的中位线,
证明:连接MN,线段MN称为△ABC的中位线,∴MN∥AB且MN=
| 1 |
| 2 |
AM2+BN2=AB2+MN2,
所以4(AM2+BN2)=4AB2+4MN2.
由于M,N是BC,AC的中点,
所以MN=
| 1 |
| 2 |
所以4MN2=AB2.
∴4(AM2+BN2)=5AB2.
点评:本题考查了中位线的平行于底边,且长度为底边的一半的性质,考查了勾股定理的运用,解本题的关键是假设M、N是中点.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目