Question

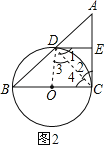
【题目】如图，已知BC是⊙O的直径，AC切⊙O于点C，AB交⊙O于点D，E为AC的中点，连结DE．

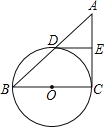
（1）若AD=DB，OC=5，求切线AC的长；

（2）求证：ED是⊙O的切线．

Answer 1

【答案】（1）10；（2）见解析

【解析】

试题分析：（1）连接CD，由直径所对的圆周角为直角可得：∠BDC=90°，即可得：CD⊥AB，然后根据AD=DB，进而可得CD是AB的垂直平分线，进而可得 AC=BC=2OC=10；

（2）连接OD，先由直角三角形中线的性质可得DE=EC，然后根据等边对等角可得∠1=∠2，由OD=OC，根据等边对等角可得∠3=∠4，然后根据切线的性质可得∠2+∠4=90°，进而可得：∠1+∠3=90°，进而可得：DE⊥OD，从而可得：ED是⊙O的切线．

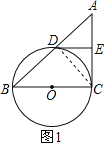
（1）解：连接CD，

∵BC是⊙O的直径，

∴∠BDC=90°，

即CD⊥AB，

∵AD=DB，OC=5，

∴CD是AB的垂直平分线，

∴AC=BC=2OC=10；

（2）证明：连接OD，如图所示，

∵∠ADC=90°，E为AC的中点，

∴DE=EC=AC，

∴∠1=∠2，

∵OD=OC，

∴∠3=∠4，

∵AC切⊙O于点C，

∴AC⊥OC，

∴∠1+∠3=∠2+∠4=90°，

即DE⊥OD，

∴ED是⊙O的切线．