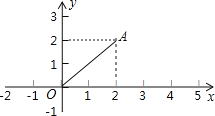题目内容
【题目】如图，直线y=kx+6与x轴、y轴分别交于点E、F，点E的坐标为（﹣3，0），点A的坐标为（﹣2.5，0）．
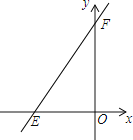
（1）求k的值；
（2）若点P（x，y）是第二象限内的直线上的一个动点，在点P的运动过程中，试写出△OPA的面积S与x的函数关系式，并写出自变量x的取值范围；
（3）探究：当点P运动到什么位置（求点P的坐标）时，△OPA的面积为5，并说明理由．
【答案】（1）k的值为2；（2）△OPA的面积S与x的函数关系式为S=2.5x+7.5（﹣3＜x＜0）；（3）点P运动到（﹣1，4）或（﹣5，﹣4）时，△OPA的面积为5．
【解析】
试题分析：（1）由直线与x轴的交点的坐标，代入即可求出k的值；（2）过点P作x轴的垂线段，能够发现P点到x轴的距离为P点的纵坐标，代入直线方程用x表示出来P点的纵坐标，再套用三角形面积公式即可得出结论，再由点P在第二象限，即可确定x的取值范围；（3）分两种情况，一种P点在x轴上方，一种在x轴下方，分类讨论即可得出结论．
解：（1）∵点E（﹣3，0）在直线y=kx+6的图象上，
∴有0=﹣3k+6，解得：k=2．
故k的值为2．
（2）过点P作PB⊥x轴，垂足为点B，如图1．
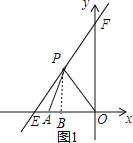
∵点P（x，y）是第二象限内的直线上的一个动点，
∴P点横坐标介于E、F的横坐标之间，
∴﹣3＜x＜0．
∵点P在直线y=2x+6上，
∴y=2x+6．
∵PB⊥x轴，且P点在第二象限，且点A的坐标为（﹣2.5，0），
∴PB=y=2x+6，OA=2.5．
∴△OPA的面积S=
OAPB=2.5x+7.5．
故△OPA的面积S与x的函数关系式为S=2.5x+7.5（﹣3＜x＜0）．
（3）∵令（2）中的关系式中x=0，解得S=7.5＞5，
∴若点P在x轴上方时，必在第二象限，点P在x轴下方时，必在第三象限．
①当点P在x轴上方时，有△OPA的面积S=2.5x+7.5，
令S=5，即2.5x+7.5，解得：x=﹣1．
此时点P的坐标为（﹣1，4）；
②当点P在x轴下方时，如图2，
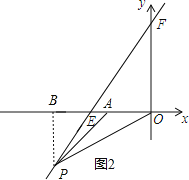
此时PB=﹣y=﹣2x﹣6，
△OPA的面积S=OAPB=×2.5×（﹣2x﹣6）=﹣2.5x﹣7.5=5，
解得：x=﹣5．
此时点P的坐标为（﹣5，﹣4）．
综上可知：点P运动到（﹣1，4）或（﹣5，﹣4）时，△OPA的面积为5．
