题目内容
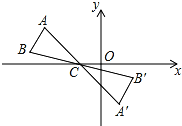
【题目】如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C的面积比为4:9.设B点的对应点B′的横坐标是2,则点B的横坐标是 .
【答案】﹣3.
【解析】
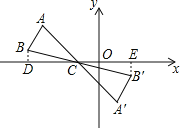
试题分析:过B和B′向x轴引垂线,构造相似比为2:3的相似三角形,那么利用相似比和所给B′的横坐标即可求得点B的横坐标.
解:过点B、B'分别作BD⊥x轴于D,B'E⊥x轴于E,
∴∠BDC=∠B'EC=90°.
∵△ABC的位似图形是△A'B'C,
∴点B、C、B'在一条直线上,
∴∠BCD=∠B'CE,
∴△BCD∽△B'CE.
∴![]() =
=![]() ,
,
又∵△ABC的位似图形△A′B′C的面积比为4:9,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
又∵点B'的横坐标是2,点C的坐标是(﹣1,0),
∴CE=3,
∴CD=![]() ×3=2,
×3=2,
∴OD=3,
∴点B的横坐标为:﹣3.
故答案为:﹣3.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目