题目内容
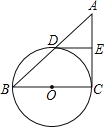
【题目】如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=2,点D是AB的中点,连接DO并延长交⊙O于点P,过点P作PF⊥AC于点F.

(1)求劣弧PC的长;(结果保留π)
(2)求阴影部分的面积.(结果保留π).
【答案】(1)![]() π;(2)
π;(2)![]() π﹣
π﹣![]() .
.
【解析】
试题分析:(1)根据垂径定理求得PD⊥AB,然后根据30°角的直角三角形的性质求得OA=2OD,进而求得OF=![]() OP,根据三角形中位线的性质求得OD=
OP,根据三角形中位线的性质求得OD=![]() BC,从而求得OA=2,然后根据弧长公式即可求得劣弧PC的长;
BC,从而求得OA=2,然后根据弧长公式即可求得劣弧PC的长;
(2)求得OF和PF,然后根据S阴影=S扇形﹣S△OPF即可求得.
解:(1)∵点D是AB的中点,PD经过圆心,
∴PD⊥AB,
∵∠A=30°,
∴∠POC=∠AOD=60°,OA=2OD,
∵PF⊥AC,
∴∠OPF=30°,
∴OF=![]() OP,
OP,
∵OA=OC,AD=BD,
∴BC=2OD,
∴OA=BC=2,
∴⊙O的半径为2,
∴劣弧PC的长=![]() =
=![]() =
=![]() π;
π;
(2)∵OF=![]() OP,
OP,
∴OF=1,
∴PF=![]() =
=![]() ,
,
∴S阴影=S扇形﹣S△OPF=![]() ﹣
﹣![]() ×1×
×1×![]() =
=![]() π﹣
π﹣![]() .
.

练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目