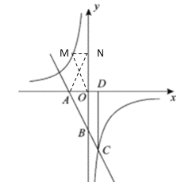
题目内容
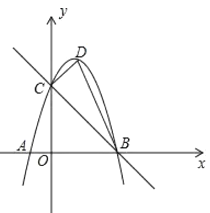
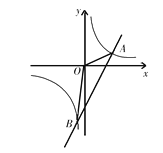
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,与反比例函数
,与反比例函数![]() 的图象在第四象限交于点
的图象在第四象限交于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求该反比例函数的表达式;
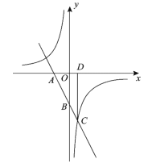
(2)点![]() 是这个反比例函数图象上的点,过点
是这个反比例函数图象上的点,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,连接
,连接![]() 、
、![]() ,如果
,如果![]() ,直接写出点
,直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)点M的坐标是(
;(2)点M的坐标是(![]() ,-20)或(-6,4).
,-20)或(-6,4).
【解析】
(1)由OA=4,OD=2得到AD=6,根据![]() 求出CD=12由此求出答案;
求出CD=12由此求出答案;
(2)设点M坐标为(x,![]() ),根据图形得到
),根据图形得到![]() ,
,![]() ,由
,由![]() 列式计算即可求出答案.
列式计算即可求出答案.
(1)∵OA=4,OD=2,
∴AD=6,
∵![]() 轴于点
轴于点![]() ,
,
∴∠ADC=90°,
∵![]() ,
,
∴CD=![]() ,
,
∴C(2,-12),
∴k=![]()
∴该反比例函数解析式为![]() ;
;
(2)设点M坐标为(x,![]() ),
),
根据图形得到![]() ,
,
∵![]() ,
,![]() ,
,
∴OB=8,
∴B(0,-8),
∵![]() ,
,![]() ,
,
∴![]() ,
,
解得x=![]() 或x=-6,
或x=-6,
当x=![]() 时,
时,![]() =-20,∴M(
=-20,∴M(![]() ,-20),
,-20),
当x=-6时,![]() =4,∴M(-6,4),
=4,∴M(-6,4),
综上,点M的坐标是(![]() ,-20)或(-6,4).
,-20)或(-6,4).

练习册系列答案
相关题目