题目内容
【题目】如图，在平面直角坐标系中，△P1OA1，△P2A1A2，△P3A2A3，…都是等腰直角三角形，其直角顶点P1(3，3)，P2，P3，…均在直线 
上．设△P1OA1，△P2A1A2，△P3A2A3，…的面积分别为 S1，S2，S3，…，依据图形所反映的规律，S2020=____．
【答案】
【解析】
分别过点
作x轴的垂线段，先根据等腰直角三角形的性质求得前三个等腰直角三角形的底边和底边上的高，继而求得三角形的面积，得出面积的规律即可得出答案．
解：如图，分别过点 作x轴的垂线段，垂足分别为点C、D、E，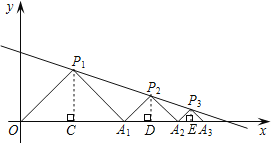
∵
（3，3），且△P1OA1是等腰直角三角形，
∴OC=CA1=P1C=3，
设
，则
，
∴OD=6+a，
∴点
坐标为（6+a，a），
将点坐标代入
得到：
，
解得：
，
∴
，
同理求得
，
，
∴
，
，
，
∴
，
因此
；
故答案为：；
天天向上一本好卷系列答案
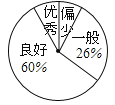
小学生10分钟应用题系列答案【题目】某校了解九年级学生近两个月“推荐书目”的阅读情况，随机抽取了该年级的部分学生，调查了他们每人“推荐书目”的阅读本数．设每名学生的阅读本数为n，并按以下规定分为四档：当n＜3时，为“偏少”；当3≤n＜5时，为“一般”；当5≤n＜8时，为“良好”；当n≥8时，为“优秀”．将调查结果统计后绘制成不完整的统计图表：
阅读本数n（本） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数（名） | 1 | 2 | 6 | 7 | 12 | x | 7 | y | 1 |
请根据以上信息回答下列问题：
（1）分别求出统计表中的x、y的值；
（2）估计该校九年级400名学生中为“优秀”档次的人数；
（3）从被调查的“优秀”档次的学生中随机抽取2名学生介绍读书体会，请用列表或画树状图的方法求抽取的2名学生中有1名阅读本数为9的概率．
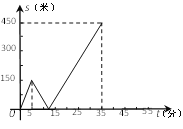
【题目】为了了解学生关注热点新闻的情况，“两会”期间，小明对班级同学一周内收看“两会”新闻的次数情况作了调查，调查结果统计如图所示（其中男生收看
次的人数没有标出）.
根据上述信息，解答下列各题：
×
（1）该班级女生人数是__________，女生收看“两会”新闻次数的中位数是________；
（2）对于某个群体，我们把一周内收看某热点新闻次数不低于次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低
，试求该班级男生人数；
（3）为进一步分析该班级男、女生收看“两会”新闻次数的特点，小明给出了男生的部分统计量（如表）.
统计量 | 平均数（次） | 中位数（次） | 众数（次） | 方差 | … |
该班级男生 |
|
|
|
| … |
根据你所学过的统计知识，适当计算女生的有关统计量，进而比较该班级男、女生收看“两会”新闻次数的波动大小.
