ЬтФПФкШн
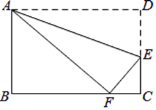
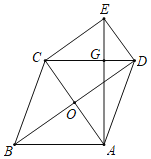
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDЕФЖдНЧЯпACЃЌBDЯрНЛгкЕуOЃЌЙ§ЕуCзїCE![]() BDЃЌЧвCEЃН
BDЃЌЧвCEЃН![]() BDЃЎ
BDЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮOCEDЪЧОиаЮЃЛ
ЃЈ2ЃЉСЌНгAEНЛCDгкЕуGЃЌШєAEЁЭCDЃЎ
ЂйЧѓsinЁЯCAGЕФжЕЃЛ
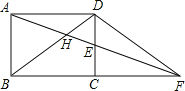
ЂкШєСтаЮABCDЕФБпГЄЮЊ6cmЃЌЕуPЮЊЯпЖЮAEЩЯвЛЖЏЕуЃЈВЛгыЕуAжиКЯЃЉЃЌСЌНгDPЃЌвЛЖЏЕуQДгЕуDГіЗЂЃЌвд1cm/sЕФЫйЖШбиЯпЖЮDPдШЫйдЫЖЏЕНЕуPЃЌдйвд![]() cm/sЕФЫйЖШбиЯпЖЮPAдШЫйдЫЖЏЕНЕуAЃЌЕНДяЕуAКѓЭЃжЙдЫЖЏЃЌЕБЕуQбиЩЯЪіТЗЯпдЫЖЏЕНЕуAЫљашвЊЕФЪБМфзюЖЬЪБЃЌЧѓAPЕФГЄКЭЕуQзпЭъШЋГЬЫљашЕФЪБМфtЃЎ
cm/sЕФЫйЖШбиЯпЖЮPAдШЫйдЫЖЏЕНЕуAЃЌЕНДяЕуAКѓЭЃжЙдЫЖЏЃЌЕБЕуQбиЩЯЪіТЗЯпдЫЖЏЕНЕуAЫљашвЊЕФЪБМфзюЖЬЪБЃЌЧѓAPЕФГЄКЭЕуQзпЭъШЋГЬЫљашЕФЪБМфtЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉЂй![]() ЃЛЂк
ЃЛЂк![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШжЄУїЫФБпаЮOCEDЪЧЦНааЫФБпаЮЃЌдйИљОнЁЯCODЃН90ЁуЭЦГіЪЧОиаЮЃЎ
ЃЈ2ЃЉЂйгЩDEЁЮACЃЌDEЃНOCЃНOAЃЌЭЦГі![]() ЃЌЩшDGЃНmЃЌдђCGЃН2mЃЌDCЃНADЃН3mЃЌЧѓГіACМДПЩНтОіЮЪЬтЃЎ
ЃЌЩшDGЃНmЃЌдђCGЃН2mЃЌDCЃНADЃН3mЃЌЧѓГіACМДПЩНтОіЮЪЬтЃЎ
ЂкЙ§ЕуPзїPTЁЭACгкTЃЎгЩsinЁЯPATЃН![]() ЃЌЭЦГіPTЃН
ЃЌЭЦГіPTЃН![]() PAЃЌгЩЕуQЕФдЫЖЏЪБМфtЃН
PAЃЌгЩЕуQЕФдЫЖЏЪБМфtЃН![]() ЃНPD+PTЃЌИљОнДЙЯпЖЮзюЖЬПЩжЊЃЌЕБDЃЌPЃЌTЙВЯпЃЌЧвDTЁЭACЪБЃЌPD+PTЕФжЕзюаЁЃЌзюаЁжЕЃНЯпЖЮODЕФГЄЃЎ
ЃНPD+PTЃЌИљОнДЙЯпЖЮзюЖЬПЩжЊЃЌЕБDЃЌPЃЌTЙВЯпЃЌЧвDTЁЭACЪБЃЌPD+PTЕФжЕзюаЁЃЌзюаЁжЕЃНЯпЖЮODЕФГЄЃЎ
ЃЈ1ЃЉжЄУїЃКЁпЫФБпаЮABCDЪЧСтаЮЃЌ
ЁрACЁЭBDЃЌOBЃНODЃЌ
ЁпECЃН![]() BDЃЌ
BDЃЌ
ЁрECЃНODЃЌ
ЁпECЁЮODЃЌ
ЁрЫФБпаЮOCEDЪЧЦНааЫФБпаЮЃЌ
ЁпЁЯCODЃН90ЁуЃЌ
ЁрЫФБпаЮOCEDЪЧОиаЮЃЎ
ЃЈ2ЃЉНтЃКЂйЁпЫФБпаЮOCEDЪЧОиаЮЃЌ
ЁрDEЁЮACЃЌDEЃНOCЃНOAЃЌ
Ёр![]() ЃЌЩшDGЃНmЃЌдђCGЃН2mЃЌDCЃНADЃН3mЃЌ
ЃЌЩшDGЃНmЃЌдђCGЃН2mЃЌDCЃНADЃН3mЃЌ
ЁпAEЁЭCDЃЌ
ЁрЁЯAGDЃНЁЯAGCЃН90ЁуЃЌ
ЁрAGЃН![]() ЃЌ
ЃЌ
ЁрACЃН![]() ЃЌ
ЃЌ
ЁрsinЁЯCAGЃН![]() ЃЎ
ЃЎ
ЂкЙ§ЕуPзїPTЁЭACгкTЃЎ
ЁпsinЁЯPATЃН![]() ЃЌ
ЃЌ
ЁрPTЃН![]() PAЃЌ
PAЃЌ
ЁпЕуQЕФдЫЖЏЪБМфtЃН![]() ЃНPD+PTЃЌ
ЃНPD+PTЃЌ
ИљОнДЙЯпЖЮзюЖЬПЩжЊЃЌЕБDЃЌPЃЌTЙВЯпЃЌЧвDTЁЭACЪБЃЌPD+PTЕФжЕзюаЁЃЌзюаЁжЕЃНЯпЖЮODЕФГЄЃЌ
гЩЃЈ2ЃЉПЩжЊ3mЃН6ЃЌ
mЃН2ЃЌ
ЁрACЃН![]() ЃЌOAЃН
ЃЌOAЃН![]() ЃЌ
ЃЌ
ЁпЁЯAODЃН90ЁуЃЌ
ЁрODЃН![]() ЃЌ
ЃЌ
ЁпDEЁЮOAЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрOPЃНPDЃН![]() ЃЌДЫЪБAPЃН
ЃЌДЫЪБAPЃН![]() ЃЌ
ЃЌ
ЁрТњзуЬѕМўЕФPAЕФжЕЮЊ![]() ЃЌЕуQзпЭъШЋГЬЫљашЕФЪБМфtЃН
ЃЌЕуQзпЭъШЋГЬЫљашЕФЪБМфtЃН![]() ЃЈsЃЉЃЎ
ЃЈsЃЉЃЎ


 бєЙтПЮЬУЭЌВНСЗЯАЯЕСаД№АИ
бєЙтПЮЬУЭЌВНСЗЯАЯЕСаД№АИ