题目内容
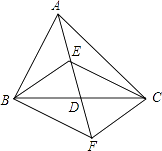
【题目】数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?
经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.
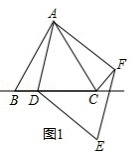
小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.
在此基础上,同学们作了进一步的研究: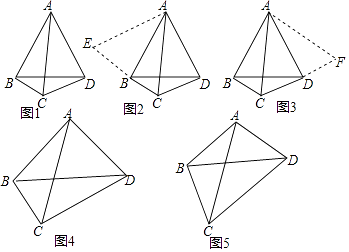
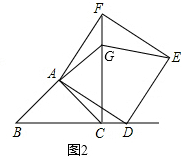
(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.
(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.
【答案】
(1)
解:BC+CD= ![]() AC;
AC;
理由:如图1,
延长CD至E,使DE=BC,
∵∠ABD=∠ADB=45°,
∴AB=AD,∠BAD=180°﹣∠ABD﹣∠ADB=90°,
∵∠ACB=∠ACD=45°,
∴∠ACB+∠ACD=45°,
∴∠BAD+∠BCD=180°,
∴∠ABC+∠ADC=180°,
∵∠ADC+∠ADE=180°,
∴∠ABC=∠ADE,
在△ABC和△ADE中, 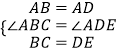 ,
,
∴△ABC≌△ADE(SAS),
∴∠ACB=∠AED=45°,AC=AE,
∴△ACE是等腰直角三角形,
∴CE= ![]() AC,
AC,
∵CE=CE+DE=CD+BC,
∴BC+CD= ![]() AC
AC
(2)
解:BC+CD=2ACcosα.理由:如图2,
延长CD至E,使DE=BC,
∵∠ABD=∠ADB=α,
∴AB=AD,∠BAD=180°﹣∠ABD﹣∠ADB=180°﹣2α,
∵∠ACB=∠ACD=α,
∴∠ACB+∠ACD=2α,
∴∠BAD+∠BCD=180°,
∴∠ABC+∠ADC=180°,
∵∠ADC+∠ADE=180°,
∴∠ABC=∠ADE,
在△ABC和△ADE中, 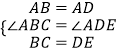 ,
,
∴△ABC≌△ADE(SAS),
∴∠ACB=∠AED=α,AC=AE,
∴∠AEC=α,
过点A作AF⊥CE于F,
∴CE=2CF,在Rt△ACF中,∠ACD=α,CF=ACcos∠ACD=ACcosα,
∴CE=2CF=2ACcosα,
∵CE=CD+DE=CD+BC,
∴BC+CD=2ACcosα

【解析】(1)先判断出∠ADE=∠ABC,即可得出△ACE是等腰三角形,再得出∠AEC=45°,即可得出等腰直角三角形,即可;(判断∠ADE=∠ABC也可以先判断出点A,B,C,D四点共圆)(2)先判断出∠ADE=∠ABC,即可得出△ACE是等腰三角形,再用三角函数即可得出结论.